
【题目】如图,在四边形ABCD中,E是AB上的一点,△ADE和△BCE都是等边三角形,点P、Q、M、N分别为AB、BC、CD、DA的中点,则四边形MNPQ是( )
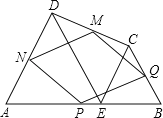
A.等腰梯形 B.矩形 C.菱形 D.正方形
【答案】C
【解析】
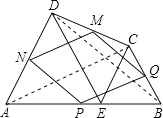
试题分析:连接AC与BD,首先证得△AEC≌△DEB,即可得到AC=BD,然后利用三角形的中位线定理证得四边形MNPQ的对边平行且相等,并且邻边相等,从而证得四边形MNPQ是菱形.
证明:连接BD、AC;
∵△ADE、△ECB是等边三角形,
∴AE=DE,EC=BE,∠AED=∠BEC=60°;
∴∠AEC=∠DEB=120°;
在△AEC与△DEB中,
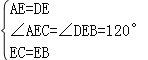 ,
,
∴△AEC≌△DEB(SAS);
∴AC=BD;
∵M、N是CD、AD的中点,
∴MN是△ACD的中位线,即MN=![]() AC,
AC,
同理可证得:NP=![]() DB,QP=
DB,QP=![]() AC,MQ=
AC,MQ=![]() BD,
BD,
∴MN=NP=PQ=MQ,
∴四边形NPQM是菱形.
故选:C.


科目:初中数学 来源: 题型:
【题目】五名学生投篮球,规定每人投20次,统计他们每人投中的次数,得到五个数据.若这五个数据的中位数是6,唯一众数是7,则他们投中次数的总和可能是( )
A. 20 B. 28 C. 30 D. 31
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中, 若∠A :∠B :∠C = 1 : 2 : 3 , 则△ABC 是( )
A. 锐角三角形. B. 直角三角形 C. 钝角三角形 D. 等腰三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABCD的四个顶点均在坐标轴上,A(0,2),∠ABC=60°.把一条长为2013个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A﹣B﹣C﹣D﹣A﹣…的规律紧绕在菱形ABCD的边上,则细线另一端所在位置的点的坐标是( )
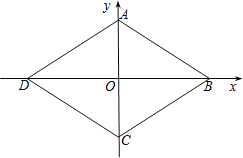
A.(![]()
![]() ,
,![]() ) B.(
) B.(![]()
![]() ,﹣
,﹣![]() ) C.(﹣
) C.(﹣![]()
![]() ,
,![]() ) D.(﹣
) D.(﹣![]() ,
,![]()
![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:①关于某条直线成轴对称的两个图形是全等图形;
②有一个外角为60°的等腰三角形是等边三角形;
③关于某直线对称的两条线段平行;
④正五边形有五条对称轴;
⑤在直角三角形中,30°角所对的边等于斜边的一半. 其中正确的有( )个.
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:①直径是弦;②经过三个点一定可以作圆;③三角形的内心到三角形各顶点的距离都相等;④半径相等的两个半圆是等弧;⑤菱形的四个顶点在同一个圆上;其中正确结论的个数有( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com