
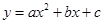 中,其函数
中,其函数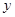 与自变量
与自变量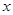 之间的部分对应值如下表所示:
之间的部分对应值如下表所示:| x | …… | 0 | 1 | 2 | 3 | 4 | 5 | …… |
| y | …… | 4 | 1 | 0 | 1 | 4 | 9 | …… |
 ,
,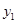 )、B(
)、B(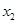 ,
,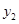 )在该函数的图象上,则当
)在该函数的图象上,则当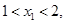
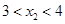 时,
时,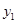 与
与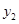 的大小关系是 ;
的大小关系是 ;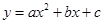 的图象上,问:当m<-3时,y1、y2、y3的值一定能作为同一个三角形三边的长吗?为什么?=】
的图象上,问:当m<-3时,y1、y2、y3的值一定能作为同一个三角形三边的长吗?为什么?=】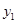 <
<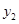 (3)
(3)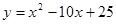 或
或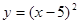 (4)当m<-3时,y1、y2、y3的值一定能作为同一个三角形三边的长
(4)当m<-3时,y1、y2、y3的值一定能作为同一个三角形三边的长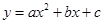
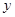 与自变量
与自变量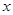 之间,则
之间,则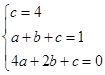 ,解得
,解得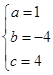 ,所以二次函数的解析式为
,所以二次函数的解析式为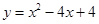 ,
,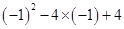 =9
=9  ,
,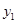 )、B(
)、B(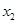 ,
,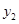 )在该函数的图象上,因为二次函数
)在该函数的图象上,因为二次函数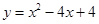 的对称轴为
的对称轴为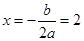 ,所以则当
,所以则当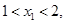
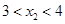 时
时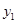 <
<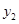
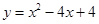 图象沿x轴向右平移3个单位
图象沿x轴向右平移3个单位 ,整理得
,整理得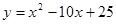 或
或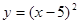
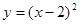 ,
,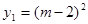 ,
,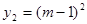 ,
,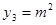 .
.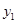 >
> >
>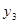 >0,
>0, 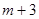 <0,
<0,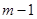 <-4<0,
<-4<0,
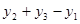 >0, ∴
>0, ∴ >
>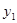


科目:初中数学 来源:不详 题型:解答题
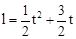 (t≥0),乙以4cm/s的速度匀速运动,半圆的长度为21cm.
(t≥0),乙以4cm/s的速度匀速运动,半圆的长度为21cm.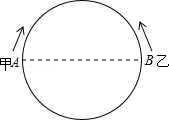
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的图象与二次函数y=ax2+x-1的图象相交于点(2,2)
的图象与二次函数y=ax2+x-1的图象相交于点(2,2)查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
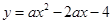 交x轴的正半轴于点A,交y轴于点B,且OA=OB.
交x轴的正半轴于点A,交y轴于点B,且OA=OB.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
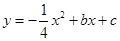 与
与 轴交于
轴交于 两点,与
两点,与 轴交于点
轴交于点 ,连结
,连结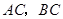 ,
, 是线段
是线段 上一动点,以
上一动点,以 为一边向右侧作正方形
为一边向右侧作正方形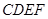 ,连结
,连结 .若
.若 ,
, .
.
 ;
; 的度数;
的度数; 点沿
点沿 轴正方向移动到点
轴正方向移动到点 时,点
时,点 也随着运动,则点
也随着运动,则点 所走过的路线长是 .
所走过的路线长是 .查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 (a≠0)的图象如图所示,则下列结论中正确的是
(a≠0)的图象如图所示,则下列结论中正确的是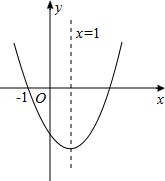
| A.ac>0 |
| B.当x>1时,y随x的增大而减小 |
| C.b﹣2a=0 |
D.x=3是关于x的方程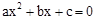 (a≠0)的一个根 (a≠0)的一个根 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 个单位后其顶点恰好在y轴上,求抛物线C的解析式及其上的不动点;
个单位后其顶点恰好在y轴上,求抛物线C的解析式及其上的不动点; 成立?若存在,求出k的值;若不存在,请说明理由.
成立?若存在,求出k的值;若不存在,请说明理由. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com