
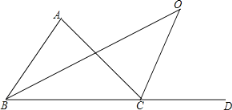
����Ŀ����ͼ,��ֱ֪��AC��BD,ֱ��AB��CD��ƽ��,��P��ֱ��AB��,�Һ͵�A��B���غ�.
(1)��ͼ�٣�����P���߶�AB��ʱ������PCA=20�㣬��PDB=30�㣬���CPD�Ķ�����
(2)��P��A��B����֮���˶�ʱ����PCA����PDB����CPD֮������ʲô���ĵ�����ϵ(ֱ��д����)��
(3)��ͼ�ڣ�����P���߶�AB���ӳ������˶�ʱ����PCA����PDB����CPD֮������ʲô���ĵ�����ϵ����˵�����ɡ�
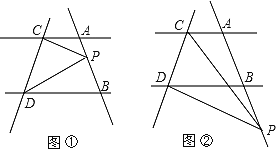
���𰸡���1��50�㣨2����CPD=��PCA+��PDB��3����CPD=��PCA-��PDB
��������
��1����ͼ�٣���P����PE��AC��CD��E�㣬����AC��BD����PE��BD������ƽ���ߵ����ʵá�CPE=��PCA=20������DPE=��PDB=30�������ԡ�CPD=50����
��2��֤�������루1��һ����
��3����ͼ�ڣ���P����PF��BD��CD��F�㣬����AC��BD����PF��AC������ƽ���ߵ����ʵá�CPF=��PCA����DPF=��PDB�����ԡ�CPD=��PCA-��PDB��
��1����ͼ�٣���P����PE��AC��CD��E�㣬
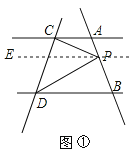
��AC��BD
��PE��BD��
���CPE=��PCA=20������DPE=��PDB=30����
���CPD=��CPE+��DPE=50����
��2����CPD=��PCA+��PDB��֤�������루1��һ������
��3����CPD=��PCA-��PDB���������£�
��ͼ�ڣ���P����PF��BD��CD��F�㣬
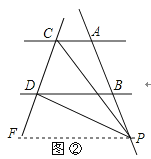
��AC��BD��
��PF��AC��
���CPF=��PCA����DPF=��PDB��
���CPD=��CPF-��DPF=��PCA-��PDB��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
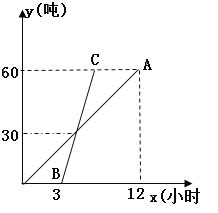
����Ŀ����ͼ���Ǽס������ֻ����˸��ݵ��Գ�����ʱ���Թ�����y���ڹ���ʱ��t�ĺ���ͼ���߶�OA��ʾ�����˵Ĺ�����y1(��)����ʱ��x(ʱ)�ĺ���ͼ���߶�BC��ʾ�һ����˵Ĺ�����y2(��)����ʱ��a(ʱ)�ĺ���ͼ����ͼ����Ϣ�ش���������⣮
(1) ���ֻ����˱����ֻ������翪ʼ����___ Сʱ�����ֻ�����ÿСʱ�Ĺ�������___�֣�
(2)ֱ��BC�ı���ʽΪ�����������������ֻ����˹���5Сʱ������ɵĹ��������������֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
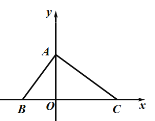
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ABO�����Ϊ8��OA��OB��BC��12����P�������ǣ�a��6����
(1) ��ABC�������������ֱ�ΪA�� �� ����B�� �� ����C�� �� ����
(2) �Ƿ���ڵ�P��ʹ��![]() �������ڣ�����������������е�P�����꣮
�������ڣ�����������������е�P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ��һ�꼶��350��ͬѧȥ���Σ���֪2��A�ͳ���1��B�ͳ�������ѧ��100�ˣ�1��A�ͳ���2��B�ͳ�������ѧ��110��.
(1)A��B�ͳ�ÿ���ɷֱ���ѧ�������ˣ�
(2)���ƻ�����A�ͳ�![]() ��������B�ͳ�
��������B�ͳ�![]() ��������������������һ����������ѧ������ǡ��ÿ����������.
��������������������һ����������ѧ������ǡ��ÿ����������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ��l��y=mx��m+1��mΪ��������m��0���������ύ��A��B���㣬����AOB��O��ԭ�㣩�����ǡΪ2�������Ҫ���ֱ��l�У� ��
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�㣨��1��y1������4��y2����һ�κ���y=3x��2��ͼ���ϣ���y1 �� y2 �� 0�Ĵ�С��ϵ�ǣ� ��
A.0��y1��y2
B.y1��0��y2
C.y1��y2��0
D.y2��0��y1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
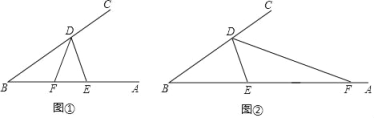
����Ŀ����֪��D��E�ֱ��ǡ�B������BC��BA�ϵĵ㣬��DEB��2��B��FΪBA��һ�㣮
��1����ͼ�٣���DFƽ�֡�BDE����֤��BD��DE+EF��
��2����ͼ�ڣ���DFΪ��DBE�����ƽ���ߣ�BD��DE��EF������������������ϵ����֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() ����ǣ�
����ǣ�![]() ��
��![]() �Ľ�ƽ���߽��ڵ�
�Ľ�ƽ���߽��ڵ�![]() .
.
��1����![]() ��
��![]() ����
����![]() ��
��![]() ��
��
��2��̽��![]() ��
��![]() ��������ϵ����˵�����ɣ�
��������ϵ����˵�����ɣ�
��3����![]() ��
��![]() ����
����![]() �Ķ���.
�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC���������������ֱ�ΪA����2��3����B����6��0����C����1��0����
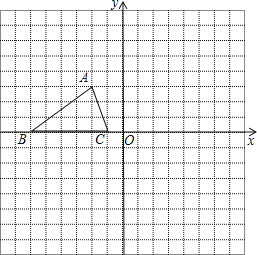
��1����ֱ��д����A����y��ԳƵĵ������Ϊ�� ��
��2������ABCƽ�ƣ�ʹ��B�ƶ��������ΪB�䣨��5����5��������ƽ�ƺ��ͼ�Ρ�A��B��C�䣻
��3������ABC������ԭ��O˳ʱ����ת90�㣬������ת���ͼ�Ρ�A��B��C�壮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com