Question

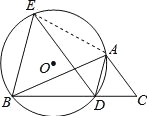
【题目】如图，已知AD是△ABC的角平分线，⊙O经过A、B、D三点，过点B作BE∥AD，交⊙O于点E，连接ED．

（1）求证：ED∥AC；

（2）连接AE，试证明：ABCD=AEAC．

Answer 1

【答案】(1)证明详见解析；(2)证明详见解析.

【解析】

试题分析：（1）由圆周角定理，可得∠BAD=∠E，又由BE∥AD，易证得∠BAD=∠ADE，然后由AD是△ABC的角平分线，证得∠CAD=∠ADE，继而证得结论；

（2）首先连接AE，易得∠CAD=∠ABE，∠ADC=∠AEB，则可证得△ADC∽△BEA，然后由相似三角形的对应边成比例，证得结论．

试题解析：（1）∵BE∥AD，

∴∠E=∠ADE，

∵∠BAD=∠E，

∴∠BAD=∠ADE，

∵AD是△ABC的角平分线，

∴∠BAD=∠CAD，

∴∠CAD=∠ADE，

∴ED∥AC；

（2）连接AE，

∵∠CAD=∠ADE，∠ADE=∠ABE，

∴∠CAD=∠ABE，

∵∠ADC+∠ADB=180°，∠ADB+∠AEB=180°，

∴∠ADC=∠AEB，

∴△ADC∽△BEA，

∴AC：AB=CD：AE，

∴ABCD=AEAC．