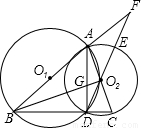
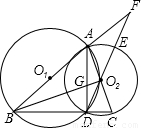
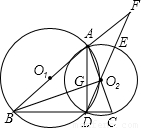
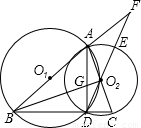
(1)证明:∵BC⊥AD于D,
∴∠BDA=∠CDA=90°,
∴AB、AC分别为⊙O
1、⊙O
2的直径,
∵∠2=∠3,∠BGD+∠2=90°,∠C+∠3=90°,
∴∠BGD=∠C;
(2)证明:∵∠DO
2C=45°,
∴∠ABD=45°,
∵O
2D=O
2C,
∴∠C=∠O
2DC=

(180-∠DO
2C)=67.5°,
∴∠4=22.5°,
∵∠O
2DC=∠ABD+∠F,
∴∠F=∠4=22.5°,
∴AD=AF;
(3)解:∵BF=6CD,
∴设CD=k,则BF=6k,
连接AE,则AE⊥AD,
∴AE∥BC,
∴△FAE∽△FBD,
∴
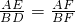
,
∴AE•BF=BD•AF,
又∵在△AO
2E和△DO
2C中,AO=DO
2,∠AOE=∠DOC,O
2E=O
2C,
∴△AO
2E≌△DO
2C,
∴AE=CD=k,
∴6k
2=BD•AF=(BC-CD)(BF-AB),
∵∠BO
2A=90°,O
2A=O
2C,
∴BC=AB,
∴6k
2=(BC-k)(6k-BC),
∴BC
2-7kBC+12k
2=0,
解得:BC=3k,或BC=4k,
当BC=3k时,BD=2k,
∵BD、BF的长是关于x的方程x
2-(4m+2)x+4m
2+8=0的两个实数根,
∴由根与系数的关系知:BD+BF=2k+6k=8k=4m+2,BD•BF=12k
2=4m
2+8,
∴k=

+

,
把BD=2k代入方程x
2-(4m+2)x+4m
2+8=0可得,4m
2-12m+29=0,
∵△=(-12)
2-4×4×29=-320<0,此方程无实数根,
∴BC=3k舍去,
当BC=4k时,BD=3k,
∴3k+6k=4m+218k
2=4m
2+8,
整理,得:m
2-8m+16=0,解得:m
1=m
2=4,
∴原方程可化为x
2-18x+72=0,
解得:x
1=6,x
2=12,
∴BD=6,BF=12.
分析:(1)运用直径所对圆周角=90°,等角的余角相等,对顶角相等证明;
(2)只需证明∠F=∠ADF即可.由A,B,D,O
2四点共圆知∠ABD=∠DO
2C=45°,∠BAD=45°,△DCO
2中,O
2C=O
2D,顶角已知,求出底角∠O
2DC的度数,∠ADF=90°-∠O
2DC,∠F=∠O
2DC-∠ABD,可知∠F=∠ABD;
(3)由已知条件,可以知道,首先应求出BD与CD的关系,这样BD与BF都用CD表示,再由根与系数的关系,求出m的值,回代方程,求出BD,BF的值,根据根的判别式进行检验.
点评:(1)在圆中证明两个角相等时,通常将它们等量转化;
(2)证明两边相等时,如果两边在同一个三角形中,则证明它们所对的角相等;
(3)本问中有四个未知量,BF,CD,BD,m,而只有三个方程BF=6CD,根与系数的关系可以列出两个,所以要根据条件先求出BD与CD的关系,这样三个未知数,三个方程可以求出结果.

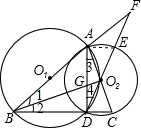
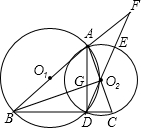 ⊙O1、⊙O2于B、C两点,延长DO2交⊙O2于E,交BA延长线于F,BO2交AD于G,连接AD.
⊙O1、⊙O2于B、C两点,延长DO2交⊙O2于E,交BA延长线于F,BO2交AD于G,连接AD. (180-∠DO2C)=67.5°,
(180-∠DO2C)=67.5°,
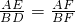 ,
, +
+ ,
,

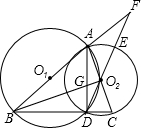 ⊙O1、⊙O2于B、C两点,延长DO2交⊙O2于E,交BA延长线于F,BO2交AD于G,连接AD.
⊙O1、⊙O2于B、C两点,延长DO2交⊙O2于E,交BA延长线于F,BO2交AD于G,连接AD.