
����Ŀ��������ɫ����ɫũ��Ʒ���г����ľ߾���������ó�̺��������г��۸�10Ԫ/ǧ���������չ���6000ǧ��Ģ�����������У�����ݺ������ṩ��Ԥ����Ϣ����ͼ�������������������⣺

��1�����������뽫����Ģ�����x���һ���Գ��ۣ� ��x�������Ģ�������۵���Ϊ Ԫ�� ����Ģ������������ ǧ�ˣ�
��2��������������Ģ����Ŷ������һ���Գ������õ������ܽ��Ϊ100000Ԫ���������ܽ����۵��ۡ�����������
��3��������Ģ����Ŷ������һ���Գ��ۿɻ�����������������Ƕ��٣�
���𰸡���1����10+0.1x��; ��6000-10x����2��100;��3�����110�����������㹽�ɻ���������16500Ԫ��
��������
�����������1�����ݵ�����ϵĢ�����г��۸�ÿ��ÿǧ������0.1Ԫ��������x�������Ģ�������۵��ۣ��ٸ���ƽ��ÿ����10ǧ�˵�Ģ��������������Ģ������������
��2�����յ�����ϵ������=�����ܽ��-�չ��ɱ�-���ַ������г�������⼴�ɣ�
��3�����ݵ�����ϵ������=�����ܽ��-�չ��ɱ�-���ַ������г�������ϵʽ�������ֵ��
�����������1����ΪĢ�����г��۸�ÿ��ÿǧ������0.1Ԫ������x�������Ģ�������۵���Ϊ��10+0.1x��Ԫ��
��Ϊ��ÿ����10ǧ�˵�Ģ��������x�������Ģ��������������6000-10x��ǧ�ˣ�
��2����������10+0.1x����6000-10x��=100000��
�����ã�x2-500x+40000=0��
�ⷽ�̵ã�x1=100��x2=400���������⣬��ȥ��
���Ժ�����������Ģ�����100���һ���Գ������õ������ܽ��Ϊ100000Ԫ��
��3��������Ϊw���������
w=��10+0.1x����6000-10x��-240x-6000��10��
=-x2+260x=-��x-130��2+16900��
��a=-1��0��
�������߿��ڷ������£�
��x=110ʱ��w���=16500��
�����110�����������㹽�ɻ���������16500Ԫ��


 �������ͬ������ϵ�д�
�������ͬ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ij�ΪAC=2cm����BC=1cm����AA��=4cm��һֻ��������س�����ı����A������B��㣬��ô������·��������·���Ƕ��٣�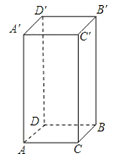
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������ε����߳��ֱ�Ϊ3 m��4 m��5 m����ô��������ε����Ϊ___.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����ж��У��Ծ��Ӳ���ķ�λ�������Ӵ���ķ�ʽ����ʾ�����磬��ƫ��30������45ǧ��λ�ã����������ϣ�������Բ��Ϊ����ʱ��ָ��ƫ��30����ʱ����1��00����ô����ص���ô���010045����ʾ�������ֱ�ʾ��ʽ����ƫ��40������78ǧ��λ�ã����ô����ʾΪ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
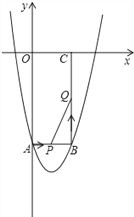
����Ŀ����12�֣���ͼ��ʾ����ƽ��ֱ������ϵxOy�У�����OABC�ı߳�OA��OC�ֱ�Ϊ12cm��6cm����A��C�ֱ���y��ĸ������x����������ϣ�������y=ax2+bx+c������A��B����18a+c=0��
��1���������ߵĽ���ʽ��
��2�������P�ɵ�A��ʼ��AB����1cm/s���ٶ����յ�B�ƶ���ͬʱ��Q�ɵ�B��ʼ��BC����2cm/s���ٶ����յ�C�ƶ���
���ƶ���ʼ���t��ʱ������PBQ�����ΪS����д��S��t֮��ĺ�����ϵʽ����д��t��ȡֵ��Χ��
����Sȡ�����ֵʱ�������������Ƿ���ڵ�R��ʹ����P��B��Q��RΪ������ı�����ƽ���ı��Σ�������ڣ����R������ꣻ��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�Ƽ�С��������һ�������ˣ����ܸ���ָ��Ҫ������н�����ת��ijһָ��涨������������ǰ������2 m��Ȼ����ת60�����������˷���ִ����һָ���ӳ�������һ�λص�ԭ���������˹����˶�����?
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com