
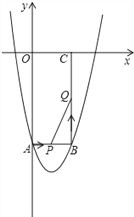
【题目】(12分)如图所示,在平面直角坐标系xOy中,矩形OABC的边长OA、OC分别为12cm、6cm,点A、C分别在y轴的负半轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A、B,且18a+c=0.
(1)求抛物线的解析式.
(2)如果点P由点A开始沿AB边以1cm/s的速度向终点B移动,同时点Q由点B开始沿BC边以2cm/s的速度向终点C移动.
①移动开始后第t秒时,设△PBQ的面积为S,试写出S与t之间的函数关系式,并写出t的取值范围.
②当S取得最大值时,在抛物线上是否存在点R,使得以P、B、Q、R为顶点的四边形是平行四边形?如果存在,求出R点的坐标;如果不存在,请说明理由.
【答案】(1)y=![]() x2-4x-12;(2)①S=-t2+6t,0<t<6;②抛物线上存在点R(3,-18),使P、B、Q、R为顶点的四边形是平行四边形.
x2-4x-12;(2)①S=-t2+6t,0<t<6;②抛物线上存在点R(3,-18),使P、B、Q、R为顶点的四边形是平行四边形.
【解析】试题分析:(1)根据矩形的对边相等求出点A、B的坐标,把两点的坐标代入抛物线解析式,再联立18a+c=0,解关于a、b、c的三元一次方程组,然后即可得到抛物线的关系式;
(2)①根据速度的不同,表示出BP、BQ的长度,然后利用三角形的面积公式列式整理即可得到S与t的关系式,根据速度分别求出点P与点Q的运动时间即可得到t取值范围;
②先根据二次函数的最大值问题求出S取最大值时的t的值,从而求出点P与点Q的坐标,再根据平行四边形的对边平行且相等,分QR与PB是对边时,PR与QB是对边时,两种情况求出点Q的坐标,然后代入抛物线解析式进行验证,如果点Q在抛物线上,则存在,否则不存在.
试题解析:(1)∵矩形OABC边长OA、OC分别为12cm和6cm,
∴点A、B的坐标分别为A(0,-12),B(6,-12),
又∵抛物线y=ax2+bx+c经过点A、B,且18a+c=0,
∴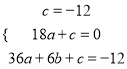 ,
,
解得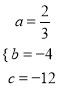 ,
,
∴抛物线解析式为y=![]() x2-4x-12;
x2-4x-12;
(2)①根据题意,PB=AB-AP=6-t,BQ=2t,
所以,S=![]() PBBQ=
PBBQ=![]() (6-t)×2t=-t2+6t,
(6-t)×2t=-t2+6t,
即S=-t2+6t,
点P运动的时间为6÷1=6秒,
点Q运动的时间为12÷2=6秒,
所以,t的取值范围是0<t<6;
②抛物线上存在点R(3,-18),使P、B、Q、R为顶点的四边形是平行四边形.
理由如下:∵S=-t2+6t=-(t-3)2+9,
∴当t=3秒时,S取最大值,
此时,PB=AB-AP=6-t=6-3=3,
BQ=2t=2×3=6,
所以,要使P、B、Q、R为顶点的四边形是平行四边形,
(i)当QR与PB是对边时,点R的横坐标是6+3=9,纵坐标是-(12-6)=-6,
所以点R的坐标为(9,-6),
此时![]() ×92-4×9-12=6≠-6,
×92-4×9-12=6≠-6,
所以点R不在抛物线上,
(ii)当PR与QB是对边时,点R的横坐标是3,纵坐标是-(12+6)=-18,
所以点R的坐标是(3,-18),
此时, ![]() ×32-4×3-12=-18,
×32-4×3-12=-18,
所以点R在抛物线上,
综上所述,抛物线上存在点R(3,-18),使P、B、Q、R为顶点的四边形是平行四边形.


科目:初中数学 来源: 题型:
【题目】我镇绿色和特色农产品在市场上颇具竞争力.外贸商胡经理按市场价格10元/千克在我区收购了6000千克蘑菇存放入冷库中.请根据胡经理提供的预测信息(如图)帮胡经理解决以下问题:

(1)若胡经理想将这批蘑菇存放x天后一次性出售, 则x天后这批蘑菇的销售单价为 元, 这批蘑菇的销售量是 千克;
(2)胡经理将这批蘑菇存放多少天后,一次性出售所得的销售总金额为100000元;(销售总金额=销售单价×销售量).
(3)将这批蘑菇存放多少天后一次性出售可获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系内,已知点A(0,6)、点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.
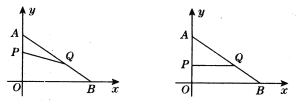
(1)求直线AB的解析式;
(2)当t为何值时,△APQ与△AOB相似?
(3)当t为何值时,△APQ的面积为![]() 个平方单位?
个平方单位?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)有四张背面图案相同的卡片A、B、C、D,其正面分别画有四个不同的几何图形(如图).小敏将这四张卡片背面朝上洗匀摸出一张,放回洗匀再摸出一张.

(1)用树状图(或列表法)表示两次摸出卡片所有可能的结果;(卡片可用A、B、C、D表示)
(2)求摸出的两张卡片图形都是中心对称图形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(2,﹣2),如果点A关于x轴的对称点是B,点B关于原点的对称点是C,那么C点的坐标是( )
A.(2,2)
B.(﹣2,2)
C.(﹣1,﹣1)
D.(﹣2,﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】连接AB,直线AB与x轴交于点C,与y轴交于点D,平面内有一点E(3,1),直线BE与x轴交于点F.直线AB的解析式记作y1=kx+b,直线BE解析式记作y2=mx+t.求:
(1)直线AB的解析式△BCF的面积;
(2)当x等于多少时,kx+b>mx+t;
当x等于多少时,kx+b<mx+t;
当x等于多少时,kx+b=mx+t;
(3)在x轴上有一动点H,使得△OBH为等腰三角形,求H的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
(1)已知n正整数,且 ![]() ,求
,求 ![]() 的值;
的值;
(2)如图,AB、CD交于点O,∠AOE=90°,若∠AOC︰∠COE=5︰4,求∠AOD的度数.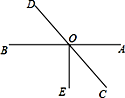
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com