
【题目】如图,已知直线AB上一点O,∠AOD=42°,∠BOC=34°,∠DOE=90°,OF平分∠COD,求∠FOD与∠EOB的度数. 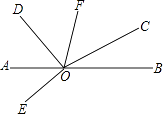
科目:初中数学 来源: 题型:
【题目】下列运算正确的是( )
A. ﹣3(a﹣b)=﹣3a﹣b B. ﹣3(a﹣b)=﹣3a+b
C. ﹣3(a﹣b)=﹣3a﹣3b D. ﹣3(a﹣b)=﹣3a+3b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,李老师出示了如下的题目:
“在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,如图,试确定线段AE与DB的大小关系,并说明理由”.
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图1,确定线段AE与DB的大小关系,请你直接写出结论:AEDB(填“>”,“<”或“=”).
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”).理由如下:如图2,过点E作EF∥BC,交AC于点F.(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,CD= (请你直接写出结果).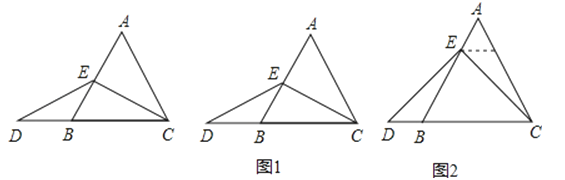
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知长方体的长为AC=2cm,宽BC=1cm,高AA′=4cm.一只蚂蚁如果沿长方体的表面从A点爬到B′点,那么沿哪条路最近?最短路程是多少?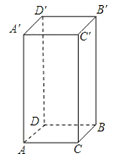
查看答案和解析>>
科目:初中数学 来源: 题型:
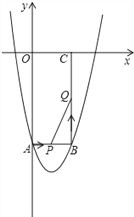
【题目】(12分)如图所示,在平面直角坐标系xOy中,矩形OABC的边长OA、OC分别为12cm、6cm,点A、C分别在y轴的负半轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A、B,且18a+c=0.
(1)求抛物线的解析式.
(2)如果点P由点A开始沿AB边以1cm/s的速度向终点B移动,同时点Q由点B开始沿BC边以2cm/s的速度向终点C移动.
①移动开始后第t秒时,设△PBQ的面积为S,试写出S与t之间的函数关系式,并写出t的取值范围.
②当S取得最大值时,在抛物线上是否存在点R,使得以P、B、Q、R为顶点的四边形是平行四边形?如果存在,求出R点的坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com