
【题目】综合题
(1)已知n正整数,且 ![]() ,求
,求 ![]() 的值;
的值;
(2)如图,AB、CD交于点O,∠AOE=90°,若∠AOC︰∠COE=5︰4,求∠AOD的度数.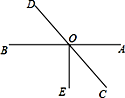
【答案】
(1)
解:原式=9a6n-4a4n=9(a2n)3-4(a2n)2
当a2n=2时,原式=9×23-16=56
(2)
解:∵∠AOE=90°,
∴∠AOC+∠EOC=90°,
∵∠AOC:∠COE=5:4,
∴∠AOC=90°× ![]() =50°,
=50°,
∴∠AOD=180°50°=130°
【解析】(1)先利用积的乘方计算,再利用积的逆运算化成含有a2n的形式,再把a2n=2代入计算即可;
(2)由于∠AOC与∠EOC互余,∠AOC:∠COE=5:4,所以∠AOC的度数可求,再根据邻补角的定义求解即可.
【考点精析】本题主要考查了角的运算和余角和补角的特征的相关知识点,需要掌握角之间可以进行加减运算;一个角可以用其他角的和或差来表示;互余、互补是指两个角的数量关系,与两个角的位置无关才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知长方体的长为AC=2cm,宽BC=1cm,高AA′=4cm.一只蚂蚁如果沿长方体的表面从A点爬到B′点,那么沿哪条路最近?最短路程是多少?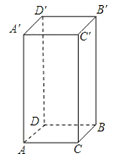
查看答案和解析>>
科目:初中数学 来源: 题型:
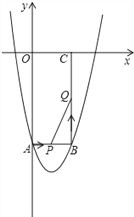
【题目】(12分)如图所示,在平面直角坐标系xOy中,矩形OABC的边长OA、OC分别为12cm、6cm,点A、C分别在y轴的负半轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A、B,且18a+c=0.
(1)求抛物线的解析式.
(2)如果点P由点A开始沿AB边以1cm/s的速度向终点B移动,同时点Q由点B开始沿BC边以2cm/s的速度向终点C移动.
①移动开始后第t秒时,设△PBQ的面积为S,试写出S与t之间的函数关系式,并写出t的取值范围.
②当S取得最大值时,在抛物线上是否存在点R,使得以P、B、Q、R为顶点的四边形是平行四边形?如果存在,求出R点的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在周长为20cm的ABCD中,AB≠AD,对角线AC、BD相交于点O,OE⊥BD交AD于E,则△ABE的周长为( )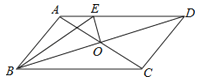
A.4cm
B.6cm
C.8cm
D.10cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某科技小组制作了一个机器人,它能根据指令要求进行行进和旋转,某一指令规定:机器人先向前方行走2 m,然后左转60°,若机器人反复执行这一指令,则从出发到第一次回到原处,机器人共走了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
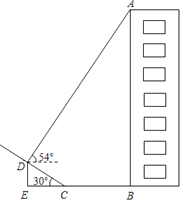
【题目】如图,某小区楼房附近有一个斜坡,小张发现楼房在水平地面与斜坡处形成的投影中,在斜坡上的影子长CD=6m,坡角到楼房的距离CB=8m.在D点处观察点A的仰角为54°,已知坡角为30°,求楼房AB的高度。(tan54°≈1.38,结果精确到0.1m)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com