
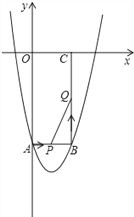
����Ŀ������AB��ֱ��AB��x�ύ�ڵ�C����y�ύ�ڵ�D��ƽ������һ��E��3��1����ֱ��BE��x�ύ�ڵ�F��ֱ��AB�Ľ���ʽ����y1=kx+b��ֱ��BE����ʽ����y2=mx+t����
��1��ֱ��AB�Ľ���ʽ��BCF�������
��2����x���ڶ���ʱ��kx+b��mx+t��
��x���ڶ���ʱ��kx+b��mx+t��
��x���ڶ���ʱ��kx+b=mx+t��
��3����x������һ����H��ʹ�á�OBHΪ���������Σ���H�����꣮
���𰸡��⣺��1���۲캯��ͼ���֪��
��C����4��0������D��0��2������B��2��3����
��C��D���������ֱ��AB�Ľ���ʽ�У��� ![]() ��
��
��ã�![]() ��
��
��ֱ��AB�Ľ���ʽΪy1=![]() x+2��
x+2��
����B��2��3����E��3��1�����뵽ֱ��BE�Ľ���ʽ�У��� ![]() ��
��
��ã� ![]() ��
��
��ֱ��BE�Ľ���ʽΪy2=��2x+7��
��y2=0������2x+7=0�����m=![]() ��
��
����F��������![]() ��0����
��0����
��CF=![]() ������4��=
������4��=![]() ��
��
���BCF�����S=![]() ��3CF=
��3CF=![]() ��3��
��3��![]() =
=![]() ��
��
��2����Ϻ���ͼ���֪��
��x��2ʱ��kx+b��mx+t����x��2ʱ��kx+b��mx+t����x=2ʱ��kx+b=mx+t��
�ʴ�Ϊ����2����2��=2��
��3�����H��������n��0����
�ߵ�O��0��0������B��2��3����
��OB= ![]() =
=![]() ��OH=|n|��BH=
��OH=|n|��BH=![]() ��
��
��OBH������������������
�ٵ�OB=OHʱ����![]() =|n|����ã�n=��
=|n|����ã�n=��![]() ��
��
��ʱ��H������Ϊ����![]() ��0����
��0����![]() ��0����
��0����
�ڵ�OB=BHʱ����![]() =
=![]() ����ã�n=0����ȥ������n=4��
����ã�n=0����ȥ������n=4��
��ʱ��H������Ϊ��4��0����
�۵�OH=BHʱ����|n|=![]() ����ã�n=
����ã�n=![]() ��
��
��ʱ��H������Ϊ��![]() ��0����
��0����
���Ͽ�֪����H������Ϊ����![]() ��0������
��0������![]() ��0������4��0����
��0������4��0����![]() ��0����
��0����
����������1�����ݹ۲�ͼ������ҳ���B��C��D�����꣬���ݴ���ϵ�����������ֱ��AB��BE�Ľ���ʽ����y2=0���������F�����꣬��������ε������ʽ���ɵó����ۣ�
��2����ֱ��AB��ͼ����ֱ��BEͼ���Ϸ�ʱ����kx+b��mx+t����ֱ��AB��ͼ����ֱ��BEͼ���·�ʱ����kx+b��mx+t�������ཻʱ����kx+b=mx+t�����ͼ�ɵó����ۣ�
��3�����H������Ϊ��n��0�����������ľ��빫ʽ�ҳ�OB��OH��BH�ij��ȣ���ϡ�OBHΪ���������ε�����������������n��ֵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����12�֣���ͼ��ʾ����ƽ��ֱ������ϵxOy�У�����OABC�ı߳�OA��OC�ֱ�Ϊ12cm��6cm����A��C�ֱ���y��ĸ������x����������ϣ�������y=ax2+bx+c������A��B����18a+c=0��
��1���������ߵĽ���ʽ��
��2�������P�ɵ�A��ʼ��AB����1cm/s���ٶ����յ�B�ƶ���ͬʱ��Q�ɵ�B��ʼ��BC����2cm/s���ٶ����յ�C�ƶ���
���ƶ���ʼ���t��ʱ������PBQ�����ΪS����д��S��t֮��ĺ�����ϵʽ����д��t��ȡֵ��Χ��
����Sȡ�����ֵʱ�������������Ƿ���ڵ�R��ʹ����P��B��Q��RΪ������ı�����ƽ���ı��Σ�������ڣ����R������ꣻ��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������κ��������ܹ��������棬ÿ��������Χ��_____���������κ�_____����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ������εĸ��߶���ȣ������ܳ���63���������ڽǺ�Ϊ900���������ı߳���________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�Ƽ�С��������һ�������ˣ����ܸ���ָ��Ҫ������н�����ת��ijһָ��涨������������ǰ������2 m��Ȼ����ת60�����������˷���ִ����һָ���ӳ�������һ�λص�ԭ���������˹����˶�����?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��4��12����ӳ�ġ��ٶ��뼤��7���ڶ̶�����Ʊ����ͻ����15.6�ڣ���Ϊ�����һ������ӰƬ����Ƭ�Ѿ����������н���ӰƬƱ����¼��15.6���ÿ�ѧ��������ʾ�ǣ�������
A. 15.6��108B. 1.56��108C. 1.56��109D. 156��108
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com