
 右图⊙I是△ABC的内切圆与AB、BC、CA分别相切于点D、E、F,G在
右图⊙I是△ABC的内切圆与AB、BC、CA分别相切于点D、E、F,G在 |
| DE |
| A、50° | B、60° |
| C、40° | D、80° |
科目:初中数学 来源: 题型:
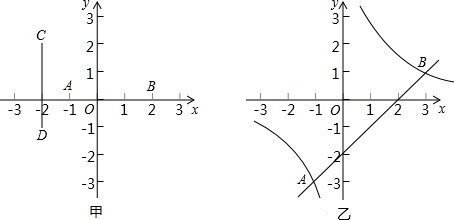
查看答案和解析>>
科目:初中数学 来源: 题型:
 在2012年日市初中学业水平考试体育学科的女子800米耐力测试中,某考点的王芳同学所跑的路程 s(米)与所用时间 t (秒)之间的函数图象为折线OBCD.和她同时起跑的李梅同学前600米的速度保持在5米/秒,后来因为体力下降,速度变慢,但还保持匀速奔跑,结果和王芳同学同时到达终点.
在2012年日市初中学业水平考试体育学科的女子800米耐力测试中,某考点的王芳同学所跑的路程 s(米)与所用时间 t (秒)之间的函数图象为折线OBCD.和她同时起跑的李梅同学前600米的速度保持在5米/秒,后来因为体力下降,速度变慢,但还保持匀速奔跑,结果和王芳同学同时到达终点.查看答案和解析>>
科目:初中数学 来源: 题型:
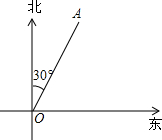 如图,一船位于航海图上的点O处向正东航行,船上工作人员测得位于船的北偏东30°方向有一灯塔A,与船的距离为24海里,若灯塔A周围20海里内有暗礁,问该船继续向东航行是否安全?请说明理由.
如图,一船位于航海图上的点O处向正东航行,船上工作人员测得位于船的北偏东30°方向有一灯塔A,与船的距离为24海里,若灯塔A周围20海里内有暗礁,问该船继续向东航行是否安全?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
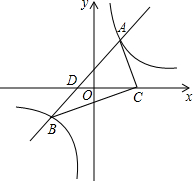 如图,在平面直角坐标系中,直线y=kx+b(k≠0)分别交双曲线y=
如图,在平面直角坐标系中,直线y=kx+b(k≠0)分别交双曲线y=| m |
| x |
| 4 |
| 5 |
| m |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 甲 | 500 | 501 | 504 | 503 | 503 | 501 | 502 | 502 | 502 | 502 |
| 乙 | 504 | 502 | 500 | 502 | 502 | 502 | 503 | 501 | 502 | 502 |
| 平均数 | 众数 | 中位数 | 方差 | |
| 甲 | 502 | 502 | 502 | 1.2 |
| 乙 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com