
 对应的点分别为A,B,点B关于点A的对称点为C,设点C表示的数为x,则
对应的点分别为A,B,点B关于点A的对称点为C,设点C表示的数为x,则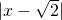 +2x=
+2x=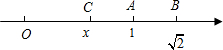


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:


| 2 |


查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
 28、
28、 阅读下列材料:
阅读下列材料:查看答案和解析>>
科目:初中数学 来源:四川省中考真题 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2008年四川省乐山市中考数学试卷(解析版) 题型:解答题


查看答案和解析>>
科目:初中数学 来源: 题型:
陈老师从拉面的制作受到启发, 设计了一个数学问题: 如图, 在数轴上截取从原点到1的对应点的线段AB, 对折后(点A与B重合)再均匀地拉成1个单位长度的线段, 这一过程称为一次操作(如在第一次操作后,原线段AB上的![]() 和
和![]() 均变成
均变成![]() ,
,![]() 变成1,等). 那么在线段AB上(除A,B)的点中, 在第n次操作后, 恰好被拉到与1重合的点所对应的数为____▲ ___.
变成1,等). 那么在线段AB上(除A,B)的点中, 在第n次操作后, 恰好被拉到与1重合的点所对应的数为____▲ ___.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com