
【题目】已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
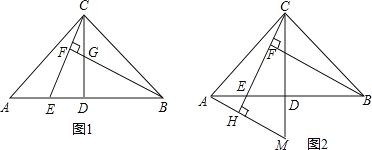
(1)直线BF垂直于直线CE于点F,交CD于点G(如图1),求证:AE=CG;
(2)直线AH垂直于直线CE,垂足为点H,交CD的延长线于点M(如图2),找出图中与BE相等的线段,并证明.
【答案】(1)见解析;(2)BE=CM.证明见解析
【解析】
试题分析:(1)首先根据点D是AB中点,∠ACB=90°,可得出∠ACD=∠BCD=45°,判断出△AEC≌△CGB,即可得出AE=CG,
(2)根据垂直的定义得出∠CMA+∠MCH=90°,∠BEC+∠MCH=90°,再根据AC=BC,∠ACM=∠CBE=45°,得出△BCE≌△CAM,进而证明出BE=CM.
(1)证明:∵点D是AB中点,AC=BC,
∠ACB=90°,
∴CD⊥AB,∠ACD=∠BCD=45°,
∴∠CAD=∠CBD=45°,
∴∠CAE=∠BCG,
又∵BF⊥CE,
∴∠CBG+∠BCF=90°,
又∵∠ACE+∠BCF=90°,
∴∠ACE=∠CBG,
在△AEC和△CGB中,
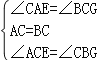
∴△AEC≌△CGB(ASA),
∴AE=CG,
(2)解:BE=CM.
证明:∵CH⊥HM,CD⊥ED,
∴∠CMA+∠MCH=90°,∠BEC+∠MCH=90°,
∴∠CMA=∠BEC,
又∵∠ACM=∠CBE=45°,
在△BCE和△CAM中,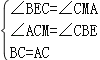 ,
,
∴△BCE≌△CAM(AAS),
∴BE=CM.


科目:初中数学 来源: 题型:
【题目】已知如图:AD∥BC,E、F分别在DC、AB延长线上.∠DCB=∠DAB,AE⊥EF,∠DEA=30°.

(1)求证:DC//AB.
(2)求∠AFE的大小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据了解,受到台风“海马”的影响,某地农作物受损面积约达35800亩,将数35800用科学记数法可表示为( )
A.0.358×105
B.3.58×104
C.35.8×103
D.358×102
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】调查初三某班同学最喜欢的球类运动,得到如图的统计图,则从图中可以( )

A.直接看出喜欢各种球类的具体人数
B.直接看出全班的总人数
C.直接看出全班同学初中三年来喜欢各种球类的变化情况
D.直接看出全班同学现在最喜欢各种球类的人数的大小关系
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把几个图形拼成一个新的图形,再通过图形面积的计算,常常可以得到一些有用的式子,或可以求出一些不规则图形的面积。
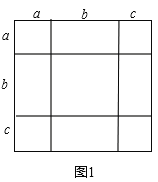
(1)如图1,是将几个面积不等的小正方形与小长方形拼成一个边长为![]() 的正方形,试用不同的方法计算这个图形的面积,你能发现什么结论,请写出来。
的正方形,试用不同的方法计算这个图形的面积,你能发现什么结论,请写出来。
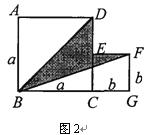
(2)如图2,是将两个边长分别为![]() 和
和![]() 的正方形拼在一起,B、C、G三点在同一直线上,连接BD和BF,若两正方形的边长满足
的正方形拼在一起,B、C、G三点在同一直线上,连接BD和BF,若两正方形的边长满足![]() ,
,![]() ,你能求出阴影部分的面积吗?
,你能求出阴影部分的面积吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,对于平面内任一点(m,n),规定以下两种变换:
①f(m,n)=(m,﹣n),如f(2,1)=(2,﹣1);
②g(m,n)=(﹣m,﹣n),如g (2,1)=(﹣2,﹣1)
按照以上变换有:f[g(3,4)]=f(﹣3,﹣4)=(﹣3,4),那么g[f(﹣3,2)]= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com