
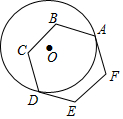
 如图,半径为1的⊙O与正六边形ABCDEF相切于点A、D,则$\widehat{AD}$的长为( )
如图,半径为1的⊙O与正六边形ABCDEF相切于点A、D,则$\widehat{AD}$的长为( )| A. | $\frac{1}{6}$π | B. | $\frac{1}{3}$π | C. | $\frac{2}{3}$π | D. | $\frac{5}{6}$π |
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:解答题
 某学校开展“科技创新大赛”活动,设计遥控车沿直线轨道做匀速直线运动的模型.现在甲、乙两车同时分别从不同起点A,B出发,沿同一轨道到达C处.设t(分)后甲、乙两遥控车与B处的距离分别为d1,d2,且d1,d2与t的函数关系如图,若甲的速度是乙的速度的1.5倍,试根据图象解决下列问题:
某学校开展“科技创新大赛”活动,设计遥控车沿直线轨道做匀速直线运动的模型.现在甲、乙两车同时分别从不同起点A,B出发,沿同一轨道到达C处.设t(分)后甲、乙两遥控车与B处的距离分别为d1,d2,且d1,d2与t的函数关系如图,若甲的速度是乙的速度的1.5倍,试根据图象解决下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)计算:20170-(-$\frac{1}{3}$)-1
(1)计算:20170-(-$\frac{1}{3}$)-1查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,∠AOB的一边OA为平面镜,∠AOB=38°,在OB上有一点E,从E点射出一束光线经OA上一点D反射,反射光线DC恰好与OB平行,则∠DEB的度数是( )
如图,∠AOB的一边OA为平面镜,∠AOB=38°,在OB上有一点E,从E点射出一束光线经OA上一点D反射,反射光线DC恰好与OB平行,则∠DEB的度数是( )| A. | 76° | B. | 52° | C. | 45° | D. | 38° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
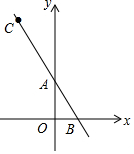 如图,过点C(-2,5)的直线AB分别交坐标轴于A(0,2),B两点,则tan∠OAB=( )
如图,过点C(-2,5)的直线AB分别交坐标轴于A(0,2),B两点,则tan∠OAB=( )| A. | $\frac{2}{5}$ | B. | $\frac{2}{3}$ | C. | $\frac{5}{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
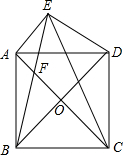 如图,正方形ABCD中,对角线AC、BD交于点O,将BD绕点B逆时针旋转30°到BE所在的位置,BE与AD交于点F,分别连接DE、CE.
如图,正方形ABCD中,对角线AC、BD交于点O,将BD绕点B逆时针旋转30°到BE所在的位置,BE与AD交于点F,分别连接DE、CE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.11×108 | B. | 1.1×108 | C. | 0.11×107 | D. | 1.1×107 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com