
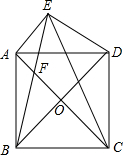
 如图,正方形ABCD中,对角线AC、BD交于点O,将BD绕点B逆时针旋转30°到BE所在的位置,BE与AD交于点F,分别连接DE、CE.
如图,正方形ABCD中,对角线AC、BD交于点O,将BD绕点B逆时针旋转30°到BE所在的位置,BE与AD交于点F,分别连接DE、CE.分析 (1)先根据旋转的性质得∠DBE=30°,BD=BE,求∠BDE=∠BED=75°,则∠EDF=75°-45°=30°,根据三角形的内角和得:∠DFE=75°,所以∠DFE=∠DEF,由等角对等边得结论;
(2)如图所示,作辅助线,构建直角三角形,根据直角三角形30°角的性质得:EG=$\frac{1}{2}$BE=$\frac{1}{2}$BD,由正方形的性质得:AC=BD,OA=$\frac{1}{2}$AC=$\frac{1}{2}$BD,根据一组对边平行且相等的四边形是平行四边形证明四边形AOGE是平行四边形,则AE∥BD;
(3)证明四边形AOGE是矩形,设EG=x,由勾股定理得:BG=$\sqrt{B{E}^{2}-E{G}^{2}}$=$\sqrt{3}$x,由矩形AOGE可知:∠EAO=90°,计算tan∠ACE的值即可.
解答 证明:(1)∵BD绕点B逆时针旋转30°到BE,
∴∠DBE=30°,BD=BE,
∴∠BDE=∠BED=$\frac{180°-30°}{2}$=75°,
在正方形ABCD中,BD是对角线,
∴∠ADB=45°,
∴∠EDF=75°-45°=30°,
在△DEF中,∠DFE=180°-∠EDF-∠FED=180°-30°-75°=75°,
∴∠DFE=∠DEF,
∴DE=DF;
(2)过E作EG⊥BD于点G,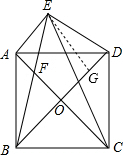
∵∠DBE=30°,
∴EG=$\frac{1}{2}$BE=$\frac{1}{2}$BD,
在正方形ABCD中,AC、BD是对角线,
∴AC=BD,OA=$\frac{1}{2}$AC=$\frac{1}{2}$BD,AC⊥BD,
∴EG=OA,且EG∥OA,
∴四边形AOGE是平行四边形,
∵∠AOD=90°,
∴四边形AOGE是矩形,
∴AE∥BD;
(3)设EG=x,则BE=BD=AC=2EG=2x,
Rt△BEG中,BG=$\sqrt{B{E}^{2}-E{G}^{2}}$=$\sqrt{3}$x,
∴OG=BG-BO=($\sqrt{3}$-1)x,
在矩形AOGE中,∠EAO=90°
∴AE=OG=($\sqrt{3}$-1)x,
∴tan∠ACE=$\frac{AE}{AC}$=$\frac{\sqrt{3}-1}{2}$.
点评 本题是四边形的综合题,难度适中,考查了正方形的性质、等腰三角形的性质和判定、矩形和平行四边形的性质和判定,熟练掌握正方形的性质是关键.


科目:初中数学 来源: 题型:选择题
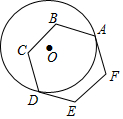 如图,半径为1的⊙O与正六边形ABCDEF相切于点A、D,则$\widehat{AD}$的长为( )
如图,半径为1的⊙O与正六边形ABCDEF相切于点A、D,则$\widehat{AD}$的长为( )| A. | $\frac{1}{6}$π | B. | $\frac{1}{3}$π | C. | $\frac{2}{3}$π | D. | $\frac{5}{6}$π |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在等边△ABC中,AB=2$\sqrt{2}$,以点A为圆心,AB为半径画$\widehat{BD}$,使得∠BAD=105°,过点C作CE⊥AD,则图中阴影部分的面积为( )
如图,在等边△ABC中,AB=2$\sqrt{2}$,以点A为圆心,AB为半径画$\widehat{BD}$,使得∠BAD=105°,过点C作CE⊥AD,则图中阴影部分的面积为( )| A. | π-2 | B. | π-1 | C. | 2π-2 | D. | 2π+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
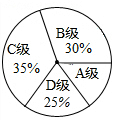 为了解某区3600名九年级学生的体育训练情况,随机抽取了区内200名九年级学生进行了一次体育模拟测试,把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格,并将测试结果绘成了如图所示的统计图,由此估计全区九年级体育测试成绩可以达到优秀的人数约为360人.
为了解某区3600名九年级学生的体育训练情况,随机抽取了区内200名九年级学生进行了一次体育模拟测试,把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格,并将测试结果绘成了如图所示的统计图,由此估计全区九年级体育测试成绩可以达到优秀的人数约为360人.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,D,E分别是边AB,AC上的点,且DE∥BC,F、G在BC上,DG∥AC,EF∥AB,DG与EF相交于点H,若S△FHG=1,S△HDE=9,则△ABC的面积为( )
如图,在△ABC中,D,E分别是边AB,AC上的点,且DE∥BC,F、G在BC上,DG∥AC,EF∥AB,DG与EF相交于点H,若S△FHG=1,S△HDE=9,则△ABC的面积为( )| A. | 100 | B. | 81 | C. | 64 | D. | 49 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com