
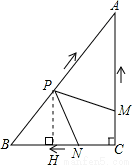
如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A,B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,设移动时间为t(单位:秒,0<t<2.5).
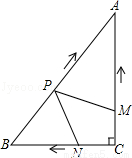
(1)当t为何值时,以A,P,M为顶点的三角形与△ABC相似?
(2)是否存在某一时刻t,使四边形APNC的面积S有最小值?若存在,求S的最小值;若不存在,请说明理由.
(1)当t=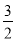 时,以A、P、M为顶点的三角形与△ABC相似;
时,以A、P、M为顶点的三角形与△ABC相似;
(2)当t= 时,四边形APNC的面积S有最小值,其最小值是
时,四边形APNC的面积S有最小值,其最小值是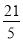
【解析】
试题分析:根据勾股定理求得AB=5cm.
(1)分类讨论:△AMP∽△ABC和△APM∽△ABC两种情况.利用相似三角形的对应边成比例来求t的值;
(2)如图,过点P作PH⊥BC于点H,构造平行线PH∥AC,由平行线分线段成比例求得以t表示的PH的值;然后根据“S=S△ABC-S△BPH”列出S与t的关系式S=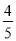 (t-
(t- )2+
)2+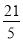 (0<t<2.5),则由二次函数最值的求法即可得到S的最小值.
(0<t<2.5),则由二次函数最值的求法即可得到S的最小值.
试题解析:∵如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.
∴根据勾股定理,得AB=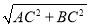 =5cm.
=5cm.
(1)以A,P,M为顶点的三角形与△ABC相似,分两种情况:
①当△AMP∽△ABC时,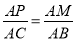 ,
,
即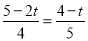 ,
,
解得t=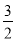 ;
;
②当△APM∽△ABC时,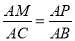 ,
,
即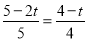 ,
,
解得t=0(不合题意,舍去);
综上所述,当t=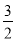 时,以A、P、M为顶点的三角形与△ABC相似;
时,以A、P、M为顶点的三角形与△ABC相似;
(2)存在某一时刻t,使四边形APNC的面积S有最小值.理由如下:
假设存在某一时刻t,使四边形APNC的面积S有最小值.
如图,过点P作PH⊥BC于点H.则PH∥AC,
∴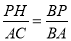 ,
,
即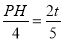 ,
,
∴PH=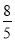 t,
t,
∴S=S△ABC-S△BPN,
=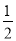 ×3×4-
×3×4-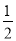 ×(3-t)•
×(3-t)•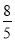 t,
t,
=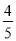 (t-
(t- )2+
)2+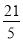 (0<t<2.5).
(0<t<2.5).
∵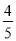 >0,
>0,
∴S有最小值.
当t= 时,S最小值是
时,S最小值是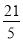 .
.
答:当t= 时,四边形APNC的面积S有最小值,其最小值是
时,四边形APNC的面积S有最小值,其最小值是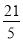 .
.
考点:相似形综合题.


科目:初中数学 来源:2014-2015学年黑龙江省鸡西市八年级上学期期中考试数学试卷(解析版) 题型:选择题
三条直线相交于同一点时,对顶角有m对,交于不同三点时,对顶角有n对,则m与n的关系是( )
A、m>n B、m=n C、m<n D、m+n=10
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级上学期期末模拟考试数学试卷(解析版) 题型:选择题
6张大小、厚度、颜色相同的卡片上分别画上线段、等边三角形、等腰梯形、平行四边形、五角星、圆.在看不见图形的条件下任意摸出1张,这张卡片上的图形是中心对称图形的概率是( )
A.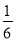 B.
B.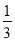 C.
C.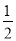 D.
D.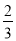
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省启东市滨海实验校共同体九年级上学期第二次质检数学试卷(解析版) 题型:解答题
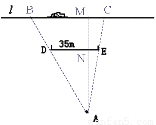
如示意图,小华家(点A处)和公路(l)之间竖立着一块35m长且平行于公路的巨型广告牌(DE).广告牌挡住了小华的视线,请在图中画出视点A的盲区,并将盲区内的那段公路计为BC.一辆以60km/h匀速行驶的汽车经过公路段的时间是3s,已知广告牌和公路的距离是40m,求小华家到公路的距离.(精确到1m)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省启东市滨海实验校共同体九年级上学期第二次质检数学试卷(解析版) 题型:填空题
函数 的图象如下图所示,则结论:
的图象如下图所示,则结论:

①两函数图象的交点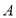 的坐标为
的坐标为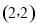 ;
;
②当 时,
时, ;
;
③当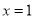 时,
时,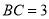 ;
;
④当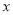 逐渐增大时,
逐渐增大时,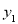 随着
随着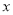 的增大而增大,
的增大而增大,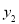 随着
随着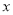 的增大而减小.
的增大而减小.
其中正确结论的序号是 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年重庆市八年级上学期期末模拟数学试卷(解析版) 题型:解答题
为弘扬中华民族传统文化,某校举办了“古诗文大赛”,并为获奖同学购买签字笔和笔记本作为奖品.1支签字笔和2个笔记本共8.5元,2支签字笔和3个笔记本共13.5元.
(1)求签字笔和笔记本的单价分别是多少元?
(2)为了激发学生的学习热情,学校决定给每名获奖同学再购买一本文学类图书,如果给每名获奖同学都买一本图书,需要花费720元;书店出台如下促销方案:购买图书总数超过50本可以享受8折优惠.学校如果多买12本,则可以享受优惠且所花钱数与原来相同.问学校获奖的同学有多少人?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省八年级上学期期中检测数学试卷(解析版) 题型:选择题
如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,EF=5,BC=8,则△EFM的周长是 ( )

A.13 B.18 C.15 D.21
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com