
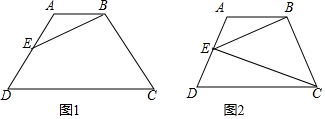
分析 (1)如图1,过点A、B分别作DC上的高线AM、BN,垂足分别是M、N,通过解直角△ADM得到DM、AM的长度,从而推知CD=3DM=3AB,所以根据梯形的面积公式进行解答;
(2)根据等腰三角形的性质和三角形内角和定理推知AE=AB;
(3)根据S梯形ABCD-S△ABE-S△DEC=S△BEC进行解答.
解答  解:(1)如图1,过点A、B分别作DC上的高线AM、BN,垂足分别是M、N,则∠AMD=90°.
解:(1)如图1,过点A、B分别作DC上的高线AM、BN,垂足分别是M、N,则∠AMD=90°.
∵在梯形ABCD中,AB∥CD,AD=BC=4,∠D=∠C=60°,
∴AB=MN、DM=CN,
∵AD=BC=4,∠D=60°,
∴AM=AD•sin60°=2$\sqrt{3}$,DM=ADcos60°=2,
又∵AB:CD=1:3,
∴CD=3DM=6,AB=2,
∴S梯形ABCD=$\frac{1}{2}$(AB+CD)•AM=$\frac{1}{2}$(2+6)×2$\sqrt{3}$=8$\sqrt{3}$;
(2)如图1,∵在梯形ABCD中,AB∥CD,
∴∠ABC+∠C=180°,∠BAD+∠D=180°,
又∠D=∠C=60°,
∴∠ABC=∠BAD=120°.
又∠EBC=90°,
∴∠ABE=30°,
∴∠AEB=180°-120°-30°=30°,即∠AEB=∠ABE,
∴AB=AE.
∵AD=4,E是AD中点,
∴AB=AE=$\frac{1}{2}$AD=2,即AB=2;
(3)如图2,过点A、B分别作DC上的高线AM、BN,垂足分别是M、N,过点E作直线GH⊥AB,交直线AB于点G,交直线CD于点H,则GH=AM.
由(1)知,AM=2$\sqrt{3}$,DM=CN=2,
则CD=4+x.
∵E是AD中点,
∴GE=EH=$\frac{1}{2}$AM=$\sqrt{3}$,
故S△BEC=S梯形ABCD-S△ABE-S△DEC,
即y=$\frac{1}{2}$(x+4+x)×2$\sqrt{3}$-$\frac{1}{2}$x•GE-$\frac{1}{2}$(x+4)•EH
=$\sqrt{3}$(2x+4)-$\frac{\sqrt{3}}{2}$x-$\frac{\sqrt{3}}{2}$(x+4)
=$\sqrt{3}$x+2$\sqrt{3}$,
即y=$\sqrt{3}$x+2$\sqrt{3}$.
点评 本题考查了四边形综合题.需要学生掌握等腰三角形的性质,三角形内角和定理,平行线的性质,三角形的面积公式和梯形的面积公式,综合性比较强.解答(3)题时,利用了“分割法”求得△BEC的面积.


科目:初中数学 来源: 题型:解答题
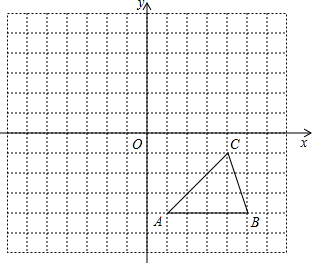 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
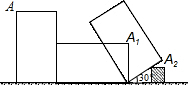 如图,小虎使一长为4cm,宽为2cm的长方形木板,在桌面上做无滑动的翻滚(顺时针方向)木板上点A位置变化为A→A1→A2,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角.若连接AA2,则线段AA2的长(精确到0.1)约为( )
如图,小虎使一长为4cm,宽为2cm的长方形木板,在桌面上做无滑动的翻滚(顺时针方向)木板上点A位置变化为A→A1→A2,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角.若连接AA2,则线段AA2的长(精确到0.1)约为( )| A. | 7.7cm | B. | 8.3cm | C. | 10.7cm | D. | 68.8cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com