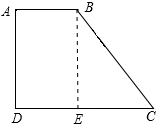
解:(1)如图,过B点作BE⊥CD,垂足为E,
在Rt△BEC中,∠BEC=90度,tanC=

,AD=BE=4,
∴tanC=

=

,CE=3,
由勾股定理可得BC=5,
∵AB=DE=2,
∴CD=5,
∴S
梯形ABCD=
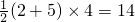
;
(2)解法一:
如图,过点P作PN⊥CD,交CD于点N,交AB的延长线于M,
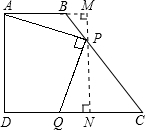
已知条件可知点P是点D沿AQ翻折而得到的,推得AP=4,
∵梯形ABCD,
∴AB∥CD,
∴∠MBP=∠C,
在Rt△BMP中,∠BMP=90度,BP=x,tan∠MBP=tan∠C=

,
可推得MP=

,BM=
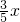
,
在Rt△AMP中,利用勾股定理可推得AM
2+MP
2=AP
2,
即
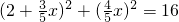
,
整理方程得5x
2+12x-60=0,
解之满足条件的
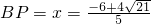
;
解法二
解:过点A作AG⊥BC,交BC的延长线于点G.
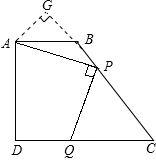
由题意可知:AP=4,
∵梯形ABCD,
∴AB∥CD,
∴∠ABG=∠C,
∵AB=2,tan∠ABG=tan∠C=

,
∴可通过解直角三角形得AG=

BG=

,
在Rt△APG中,利用勾股定理可得AG
2+GP
2=AP
2,
即
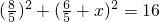
,
化简得5x
2+12x-60=0,
以下解法同上.
解法三:
解:如图,延长AP与DC相交于点F,
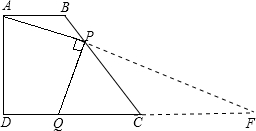
可推得AP=4,
由已知可得AB=2,BP=x,CP=5-x,
利用相似三角形的知识或平行线截线段成比例,
定理可得
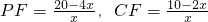
,
在Rt△ADF中,∠D=90度,AD
2+DF
2=AF
2,
即
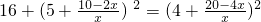
.
化简得5x
2+12x-60=0,以下解法同解法一、二.
分析:(1)过B点作BE⊥CD,垂足为E,根据∠C的正切值可以求出CE的长度,然后利用勾股定理即可求出BC的长度;先求出CD的长度,再利用梯形的面积公式进行求解即可;
(2)过点P作PN⊥CD,交CD于点N,交AB的延长线于M,根据题意可以看做点P是点Q沿AQ翻折而得到的,根据翻折的对称性,AP=AD,再设BP=x,利用∠C的正切值表示出PM,BM,然后在△APM中,利用勾股定理列式计算即可求出BP的长度.
点评:本题考查了直角梯形,勾股定理以及解直角三角形的知识,是综合题,仔细分析图形作出辅助线是解题的关键.

 ,∠ADC=∠DAB=90°,P是腰BC上一个动点(不含点B、C),作PQ⊥AP交CD于点Q(图1)
,∠ADC=∠DAB=90°,P是腰BC上一个动点(不含点B、C),作PQ⊥AP交CD于点Q(图1)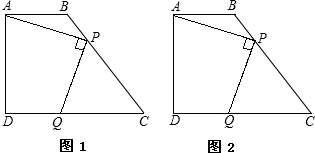
 解:(1)如图,过B点作BE⊥CD,垂足为E,
解:(1)如图,过B点作BE⊥CD,垂足为E, ,AD=BE=4,
,AD=BE=4, =
= ,CE=3,
,CE=3,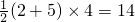 ;
;
 ,
, ,BM=
,BM=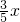 ,
,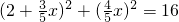 ,
,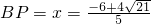 ;
;
 ,
, BG=
BG= ,
,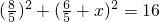 ,
,
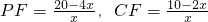 ,
,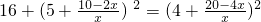 .
.

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )
如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )