
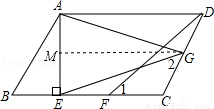
已知,如图,在 中,AE⊥ BC,垂足为E,点F为CE上的一点,点G为CD上的一点,CF=CG,连接DF、EG、AG, AG=EG,∠ 1=∠ 2.
中,AE⊥ BC,垂足为E,点F为CE上的一点,点G为CD上的一点,CF=CG,连接DF、EG、AG, AG=EG,∠ 1=∠ 2.

(1)若CE=4,AE=3,求BE的长;
(2)求证:∠CEG= ∠ AGE.
∠ AGE.
(1)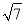 ;(2)见解析.
;(2)见解析.
【解析】
试题分析:(1)根据所给的条件可证得△DFC≌△EGC,根据全等三角形的性质可得CD=CE=4,因为四边形ABCD是平行四边形,所以AB=CD=4, 在Rt△ABE中,由勾股定理求得BE即可;
(2)过G作GM⊥AE于点M,根据AE⊥BC,可得∠EMG=∠AEB=90°,所以GM∥BC, 根据平行的性质可得∠EGM=∠CEG,再有AG=EG,可得∠EGM=∠AGM= ∠AGE,所以∠CEG=
∠AGE,所以∠CEG= ∠AGE.
∠AGE.
试题解析:(1)【解析】
∵在△DFC和△EGC中,

∴△DFC≌△EGC(ASA),
∴CD=CE=4,
∵四边形ABCD是平行四边形,
∴AB=CD=4,
∵AE⊥ BC,
∴∠AEB=90°,
在Rt△ABE中,由勾股定理得:BE=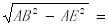
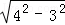 =
=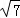 ;
;
(2)证明:过G作GM⊥AE于点M,
∵AE⊥BC,
∴∠EMG=∠AEB=90°,
∴GM∥BC,
∴∠EGM=∠CEG,
∵AG=EG,
∴∠EGM=∠AGM= ∠AGE
∠AGE
∴∠CEG= ∠AGE.
∠AGE.
考点:1.平行四边形的性质;2.三角形全等的判定和性质;3.勾股定理的应用;4.等腰三角形的性质


科目:初中数学 来源:2014年沪教版初中数学九年级下册第二十八章28.1统计的意义练习卷(解析版) 题型:选择题
今年我市有近4万名考生参加中考,为了解这些考生的数学成绩,从中抽取1000名考生的数学成绩进行统计分析,以下说法正确的是( )
A.这1000名考生是总体的一个样本
B.近4万名考生是总体
C.每位考生的数学成绩是个体
D.1000名学生是样本容量
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西钦州卷)数学(解析版) 题型:填空题
如图,△ABC中,∠A=40°,AB的垂直平分线MN交AC于点D,∠DBC=30°,若AB=m,BC=n,则△DBC的周长为 .

查看答案和解析>>
科目:初中数学 来源:2014年青岛版初中数学七年级上册第一章1.3线段、直线和射线练习卷(解析版) 题型:填空题
点A1,A2,A3…A6是线段AB上6个不同的点,由这些点和端点A、B共可构成_______条不同的线段.
查看答案和解析>>
科目:初中数学 来源:2014年沪教版初中数学九年级下册第二十八章28.2基本的统计量练习卷(解析版) 题型:填空题
有一组数据:2,3,5,5,x,它们的平均数是10,则这组数据的众数是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com