【题目】已知线段AB=20cm，直线AB上有一点C，且BC=6cm，点M是线段AB的中点，点N是线段BC的中点，则MN= cm．
【答案】7或13．
【解析】
试题分析：根据中点的定义，可分别求出AM、BN的长度，点C存在两种情况，一种在线段AB上，一种在线段AB外，分类讨论，即可得出结论．
解：依题意可知，C点存在两种情况，一种在线段AB上，一种在线段AB外．
①C点在线段AB上，如图1：
∵点M是线段AB的中点，点N是线段BC的中点，
∴AM=
=10cm，BN=
=3cm，
MN=AB﹣AM﹣BN=20﹣10﹣3=7cm．
②C点在线段AB外，如图2：
∵点M是线段AB的中点，点N是线段BC的中点，
∴AM=
=10cm，BN=
=3cm，
MN=AB﹣AM+BN=20﹣10+3=13cm．
综上得MN得长为7cm或者13cm．
故答案为：7或13．
名校课堂系列答案科目：初中数学 来源： 题型：
【题目】已知二次函数y=x2﹣4x+3．
（1）把这个二次函数化成y=a（x﹣h）2+k的形式；
（2）写出二次函数的对称轴和顶点坐标；
（3）求二次函数与x轴的交点坐标；
（4）画出这个二次函数的图象；
（5）观察图象并写出y随x增大而减小时自变量x的取值范围．
（6）观察图象并写出当x为何值时，y＞0．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平整的地面上，有若干个完全相同的棱长的小正方体堆成一个几何体（如图所示）．
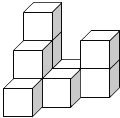
（1）这个几何体由 个小正方体组成，请画出这个几何体的三视图；
（2）如果在这个几何体的表面喷上黄色的漆，则在所有的小正方体中，有 个正方体只有两个面是黄色，有 个正方体只有三个面是黄色（注：该几何体与地面重合的部分不喷漆）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知直线l的解析式为y=
x﹣1，抛物线y=ax2+bx+2经过点A（m，0），B（2，0），D（1，
）三点．
（1）求抛物线的解析式及A点的坐标，并在图示坐标系中画出抛物线的大致图象；
（2）已知点 P（x，y）为抛物线在第二象限部分上的一个动点，过点P作PE垂直x轴于点E，延长PE与直线l交于点F，请你将四边形PAFB的面积S表示为点P的横坐标x的函数，并求出S的最大值及S最大时点P的坐标；
（3）将（2）中S最大时的点P与点B相连，求证：直线l上的任意一点关于x轴的对称点一定在PB所在直线上．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
