
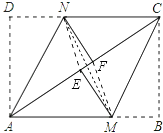
����Ŀ����ͼ��1�����ھ���ABCD�У��ѡ�B����D�ֱ��ۣ�ʹ��B��Dǡ�����ڶԽ���AC�ϵĵ�E��F�����ۺ۷ֱ�ΪCM��AN�� 
��1����֤����ADN�ա�CBM��
��2��������MF��NE��֤���ı���MFNE��ƽ���ı��Σ��ı���MFNE����������˵�����ɣ�
��3����P��Q�Ǿ��εı�CD��AB�ϵ����㣬����PQ��CQ��MN����ͼ��2����ʾ����PQ=CQ��PQ��MN����AB=4cm��BC=3cm����PC�ij��ȣ�
���𰸡�
��1��֤�������۵������ʵó���DAN=��NAC����BCM=��ACM��
��AD��BC��
���DAC=��BCA��
���DAN=��BCM��
��Rt��ADN��Rt��CBM��
��  ��
��
���ADN�ա�CBM
��2���⣺����NE��MF��
�ߡ�ADN�ա�CBM��
��NF=ME��
�ߡ�NFE=��MEF��
��NF��ME��
���ı���MFNE��ƽ���ı��Σ�
��MN��EF����ֱ��
���ı���MFNE��������
��3���⣺��AC��MN�Ľ���ΪO��EF=x����QG��PC��G�㣬
��AB=4��BC=3��
��AC=5��
��AF=CE=BC=3��
��2AF��EF=AC����6��x=5��
���x=1��
��EF=1��
��CF=2��
��Rt��CFN��tan��NCF= ![]() ��
��
���NF= ![]() ��
��
��OE=OF= ![]() EF=
EF= ![]() ��
��
����Rt��NFO��ON2=OF2+NF2��
��ON= ![]() ��
��
��MN=2ON= ![]() ��
��
��PQ��MN��PN��MQ��
���ı���MQPN��ƽ���ı��Σ�
��MN=PQ= ![]() ��
��
��PQ=CQ��
���PQC�ǵ��������Σ�
��PG=CG��
��Rt��QPG��
PG2=PQ2��QG2����PG= ![]() =1��
=1��
��PC=2PG=2��
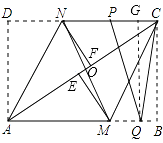
����������1�������۵������ʵó���DAN=��NAC����BCM=��ACM���Ӷ�����AD��BC�ɵó���DAN=��BCM���Ӷ������жϳ���ADN�ա�CBM����2������NE��MF�����ݣ�1���Ľ��ۿɵó�NF=ME�����ɡ�NFE=��MEF���жϳ�NF��ME����ֱ��������NFE�У�NEΪб�ߣ�NFΪֱ�DZߣ����ж��ı���MFNE�������Σ���3����AC��MN�Ľ���ΪO��EF=x����QG��PC��G�㣬�������AC=5�����ݷ��۱任֪��AF=CE=3�����ǿɵ�AF+��CE��EF��=5���ɵ�EF=1����Rt��CFN�У�NF=tan��NCFCF����Rt��NFE�У�NO2=NF2+OF2 �� ���NO�ij�����NM=PQ=QC=2NO��PC=2 ![]() ��
��
�����㾫�������ڱ��⿼���ƽ���ı��ε��ж������ε��ж���������Ҫ�˽�����Ա߷ֱ�ƽ�е��ı�����ƽ���ı��Σ�����Ա߷ֱ���ȵ��ı�����ƽ���ı��Σ�һ��Ա�ƽ������ȵ��ı�����ƽ���ı��Σ�����ԽǷֱ���ȵ��ı�����ƽ���ı��Σ��Խ�����ƽ�ֵ��ı�����ƽ���ı��Σ�����һ���ı��Σ��ı���ȳ����Σ��ı��εĶԽ��ߣ���ֱ���������Σ���֪ƽ���ı��Σ��ڱ���Ƚ����Σ����Խ�������ֱ��˳������Ϊ���β��ܵó���ȷ�𰸣�


 ͬ����ϰǿ����չϵ�д�
ͬ����ϰǿ����չϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������������У���ABC�����㶼�ڸ���ϣ���A��C������ֱ�Ϊ����5��1��������1��4�������������ƽ��ֱ������ϵ����������⣺ 
��1��������ABC����y��ԳƵġ�A1B1C1��
��2��������ABC����ԭ��O�ԳƵġ�A2B2C2��
��3����C1������������C2������������C��C1��C2�����Բ��Բ�� ![]() �ij����������У���
�ij�������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������OA��BA�ֱ��ʾ�ס������������г��˶����̵�һ�κ�����ͼ��ͼ��s��t�ֱ��ʾ��ʻ�����ʱ�䣬�������������г����ٶ����km/h�� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AD��BC���Խ���AC���е�ΪO������O��AC�Ĵ��߷ֱ���AD��BC�ཻ�ڵ�E��F������AF����֤��AE=AF�� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������С���Ӽ��������г���ͬѧ��ȥ�棬Ȼ�أ�ͼ������ҵ�·��y��ǧ�ף���ʱ��x�����ӣ��ĺ���ͼ����ͼ����Ϣ������˵����һ����ȷ���ǣ� �� 
A.С����ͬѧ�ҵ�·����3ǧ��
B.С����ͬѧ�Ҷ�����ʱ����1Сʱ
C.С��ȥʱ������·���ؼ�ʱ������·
D.С���ؼ�ʱ�õ�ʱ���ȥʱ�õ�ʱ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͬһֱ������ϵ�У�����y=mx+m��y=��mx2+2x+2��m�dz�������m��0����ͼ������ǣ� ��
A.
B.
C.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC���������������ֱ�ΪA����6��0����B����2��3����
C����1��0����
��1����ֱ��д�����B��������ԭ��O�ĶԳƵ�B1�����ꣻ
��2������ABC������ԭ��O��ʱ����ת90�㣮������Ӧ�ġ�A��B��C��ͼ�Σ�ֱ��д����A�Ķ�Ӧ��A������ꣻ
��3�����ı���A��B��C��D��Ϊƽ���ı��Σ���ֱ��д�����ĸ�����D������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����y=2x��y=��x��ͼ��ֱ�Ϊֱ��l1 �� l2 �� ���㣨1��0����x��Ĵ��߽�l1�ڵ�A1 �� ����A1��y��Ĵ��߽�l2�ڵ�A2 �� ����A2��x��Ĵ��߽�l1�ڵ�A3 �� ����A3��y��Ĵ��߽�l2�ڵ�A4 �� �����ν�����ȥ�����A2017������Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB�ǡ�O��ֱ������C��D�ڡ�O�ϣ���AB=6����CAB=30�� 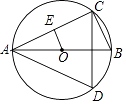
��1�����ADC�Ķ�����
��2�����OE��AC������ΪE����OE�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com