
【题目】如图,已知AB是⊙O的直径,点C,D在⊙O上,且AB=6,∠CAB=30° 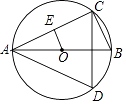
(1)求∠ADC的度数;
(2)如果OE⊥AC,垂足为E,求OE的长.
【答案】
(1)解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵AB=6,BC=3,
∴cosB= ![]() =
= ![]() ,
,
∴∠B=60°,
∴∠ADC=60°
(2)解:∵OE⊥AC,
∴AE=CE,
∴OE为△ABC的中位线,
∵AB=6,∠CAB=30°,
∴BC=3
∴OE= ![]() BC=
BC= ![]()
【解析】(1)由AB是⊙O的直径,根据圆周角定理的推论得到∠ACB=90°,在Rt△ABC中,理由∠B的余弦可求出∠B=60°,然后根据圆周角定理得到∠ADC=60°;(2)由于OE⊥AC,根据垂径定理得到AE=CE,则OE为△ABC的中位线,所以OE= ![]() BC=
BC= ![]() .
.
【考点精析】利用勾股定理的概念和垂径定理对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.


科目:初中数学 来源: 题型:
【题目】如图(1),在矩形ABCD中,把∠B、∠D分别翻折,使点B、D恰好落在对角线AC上的点E、F处,折痕分别为CM、AN, 
(1)求证:△ADN≌△CBM;
(2)请连接MF、NE,证明四边形MFNE是平行四边形;四边形MFNE是菱形吗?请说明理由;
(3)点P、Q是矩形的边CD、AB上的两点,连接PQ、CQ、MN,如图(2)所示,若PQ=CQ,PQ∥MN,且AB=4cm,BC=3cm,求PC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校是乒乓球体育传统项目学校,为进一步推动该项目的开展,学校准备到体育用品店购买直拍球拍和横拍球拍若干副,并且每买一副球拍必须要买10个乒乓球,乒乓球的单价为2元/个,若购买20副直拍球拍和15副横拍球拍花费9000元;购买10副横拍球拍比购买5副直拍球拍多花费1600元.
(1)求两种球拍每副各多少元?
(2)若学校购买两种球拍共40副,且直拍球拍的数量不多于横拍球拍数量的3倍,请你给出一种费用最少的方案,并求出该方案所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC、CD,测得BC=6米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,试求电线杆的高度(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD内接于⊙O, ![]() :
: ![]() :
: ![]() =2:3:5,∠BAD=120°,则∠ABC的度数为( )
=2:3:5,∠BAD=120°,则∠ABC的度数为( )
A.100°
B.105°
C.120°
D.125°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知Rt△AEC中,∠E=90°,请按如下要求进行操作和判断: 
(1)尺规作图:作△AEC的外接圆⊙O,并标出圆心O(不写画法);
(2)延长CE,在CE的延长线上取点B,使EB=EC,连结AB,设AB与⊙O的交点为D(标出字母B、D),判断:图中 ![]() 与
与 ![]() 相等吗?请说明理由.
相等吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,下列结论正确的有( )
①AD=BD=BC;
②△BCD∽△ABC;
③AD2=ACDC;
④点D是AC的黄金分割点.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为原点,点A(4,0),点B(0,3),把△ABO绕点B逆时针旋转,得△A′BO′,点A,O旋转后的对应点为A′,O′,记旋转角为α.
(1)如图①,若α=90°,求AA′的长;
(2)如图②,若α=120°,求点O′的坐标;
(3)在(Ⅱ)的条件下,边OA上 的一点P旋转后的对应点为P′,当O′P+BP′取得最小值时,求点P′的坐标(直接写出结果即可)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com