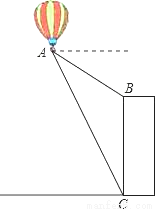
如图，热气球的探测器显示，从热气球A看一栋大楼顶部B的俯角为30°，看这栋大楼底部C的俯角为60°．热气球A的高度为240米，求这栋大楼的高度．
举一反三单元同步过关卷系列答案科目：初中数学 来源：2016届山东省泰安市泰山区中考模拟数学试卷（解析版） 题型：选择题
根据下表中关于二次函数y=ax2+bx+c的自变量x与函数y的对应值，可判断二次函数的图象与x轴（ ）
x | … | -1 | 0 | 1 | 2 | … |
y | … | -1 |
| -2 |
| … |
A．只有一个交点
B．有两个交点，且它们分别在y轴两侧
C．有两个交点，且它们均在y轴同侧
D．无交点
查看答案和解析>>
科目：初中数学 来源：2016届山东省滨州市中考一模数学试卷（解析版） 题型：解答题
如图，已知抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=-1，且抛物线经过A（1，0），C（0，3）两点，与x轴交于点B．
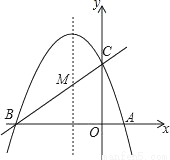
（1）若直线y=mx+n经过B、C两点，求直线BC和抛物线的解析式；
（2）在抛物线的对称轴x=-1上找一点M，使点M到点A的距离与到点C的距离之和最小，求出点M的坐标；
（3）设点P为抛物线的对称轴x=-1上的一个动点，求使△BPC为直角三角形的点P的坐标．
查看答案和解析>>
科目：初中数学 来源：2016届山东省滨州市中考一模数学试卷（解析版） 题型：选择题
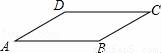
如图，已知平行四边形ABCD中，AB=3，AD=2，∠B=150°，则平行四边形ABCD的面积为（ ）
A．2 B．3 C．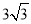
D．6
查看答案和解析>>
科目：初中数学 来源：2016届山东省青岛市中考二模数学试卷（解析版） 题型：解答题
【问题情境】
张老师给爱好学习的小林和小兰提出这样一个问题：如图①，在△ABC中，AB=AC，点P为边BC上的任一点，过点P作PD⊥AB，PE⊥AC，垂足分别为D、E，过点C作CF⊥AB，垂足为F．求证：PD+PE=CF．
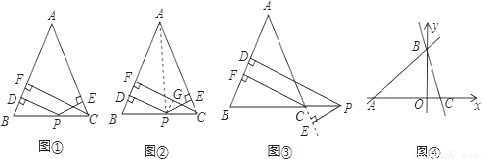
小林的证明思路是：如图②，连接AP，由△ABP与△ACP面积之和等于△ABC的面积可以证得：PD+PE=CF．
小兰的证明思路是：如图②，过点P作PG⊥CF，垂足为G，通过证明四边形PDFG是矩形，
可得：PD=GF，PE=CG，则PD+PE=CF．
【变式探究】如图③，当点P在BC延长线上时，其余条件不变，求证：PD-PE=CF；
【结论运用】请运用上述解答中所积累的经验和方法完成下列两题：
如图④，在平面直角坐标系中有两条直线l1：y=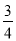
x+3、l2：y=-3x+3，若l2上的一点M到l1的距离是1，请运用上述的结论求出点M的坐标．
查看答案和解析>>
科目：初中数学 来源：2016届山东省青岛市中考二模数学试卷（解析版） 题型：填空题
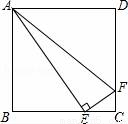
如图，正方形ABCD的边长为4，E、F分别是BC、CD上的两个动点，且AE⊥EF．则AF的最小值是 ．
查看答案和解析>>
科目：初中数学 来源：2016届山东省青岛市中考二模数学试卷（解析版） 题型：选择题
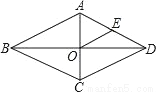
如图，菱形中，对角线AC、BD交于点O，E为AD边中点，菱形ABCD的周长为28，则OE的长等于（ ）
A．3.5 B．4 C．7 D．14
查看答案和解析>>
科目：初中数学 来源：2016届山东省德州市德城区中考二模数学试卷（解析版） 题型：选择题
对于点A（x1，y1）、B（x2，y2），定义一种运算：A⊕B=（x1+x2）+（y1+y2）．例如，A（-5，4），B（2，-3），A⊕B=（-5+2）+（4-3）=-2．若互不重合的四点C，D，E，F，满足C⊕D=D⊕E=E⊕F=F⊕D，则C，D，E，F四点（ ）
A．在同一条直线上
B．在同一条抛物线上
C．在同一反比例函数图象上
D．是同一个正方形的四个顶点
查看答案和解析>>
科目：初中数学 来源：2016届山东省聊城市东昌府区中考一模数学试卷（解析版） 题型：填空题
如图，在平面直角坐标系中，将矩形AOCD沿直线AE折叠（点E在边DC上），折叠后端点D恰好落在边OC上的点F处．若点D的坐标为（10，8），则点E的坐标为 ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
