
【问题情境】
张老师给爱好学习的小林和小兰提出这样一个问题:如图①,在△ABC中,AB=AC,点P为边BC上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D、E,过点C作CF⊥AB,垂足为F.求证:PD+PE=CF.
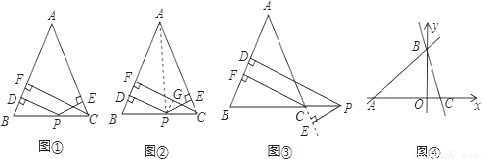
小林的证明思路是:如图②,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.
小兰的证明思路是:如图②,过点P作PG⊥CF,垂足为G,通过证明四边形PDFG是矩形,
可得:PD=GF,PE=CG,则PD+PE=CF.
【变式探究】如图③,当点P在BC延长线上时,其余条件不变,求证:PD-PE=CF;
【结论运用】请运用上述解答中所积累的经验和方法完成下列两题:
如图④,在平面直角坐标系中有两条直线l1:y=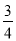 x+3、l2:y=-3x+3,若l2上的一点M到l1的距离是1,请运用上述的结论求出点M的坐标.
x+3、l2:y=-3x+3,若l2上的一点M到l1的距离是1,请运用上述的结论求出点M的坐标.
科目:初中数学 来源:2016届山东省泰安市泰山区中考模拟数学试卷(解析版) 题型:解答题
张老师和李老师同时从学校出发,步行15千米去县城购买书籍,张老师比李老师每小时多走1千米,结果比李老师早到半小时,两位老师每小时各走多少千米?
查看答案和解析>>
科目:初中数学 来源:2016届山东省济宁市邹城市中考一模数学试卷(解析版) 题型:选择题
下列运算正确的是( )
A.(2a2)3=6a6
B.-a2b2•3ab3=-3a2b5
C.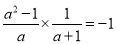
D.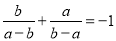
查看答案和解析>>
科目:初中数学 来源:2016届山东省滨州市中考一模数学试卷(解析版) 题型:选择题
如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:(1)AE=BF;(2)AE⊥BF;(3)AO=OE;(4)S△AOB=S四边形DEOF中正确的有( )
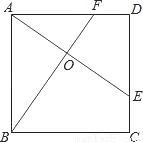
A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
科目:初中数学 来源:2016届山东省滨州市中考一模数学试卷(解析版) 题型:选择题
下列事件是随机事件的是( )
A.明天太阳从东方升起
B.任意画一个三角形,其内角和是360°
C.通常温度降到0℃以下,纯净的水结冰
D.射击运动员射击一次,命中靶心
查看答案和解析>>
科目:初中数学 来源:2016届山东省青岛市中考二模数学试卷(解析版) 题型:解答题
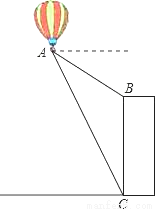
如图,热气球的探测器显示,从热气球A看一栋大楼顶部B的俯角为30°,看这栋大楼底部C的俯角为60°.热气球A的高度为240米,求这栋大楼的高度.
查看答案和解析>>
科目:初中数学 来源:2016届山东省青岛市中考二模数学试卷(解析版) 题型:填空题
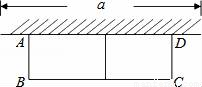
已知:如图,有长为24米的篱笆,一面利用墙(墙的最大可用长度a为10米),围成中间隔有一道篱笆的长方形花圃.设花圃的宽AB为x米,面积为S米2.则S与x的函数关系式 ;自变量的取值范围 .
查看答案和解析>>
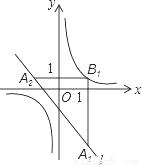
科目:初中数学 来源:2016届山东省德州市德城区中考二模数学试卷(解析版) 题型:填空题
如图,在平面直角坐标系中,已知直线l:y=-x-1,双曲线y=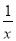 .在直线l上取点A1,过点A1作x轴的垂线交双曲线于点B1,过点B1作y轴的垂线交直线l于点A2,继续操作:过点A2作x轴的垂线交双曲线于点B2,过点B2作y轴的垂线交直线l于点A3,…,依次这样得到双曲线上的点B1,B2,B3,B4,…,Bn.记点A1的横坐标为2,则B2016的坐标为 .
.在直线l上取点A1,过点A1作x轴的垂线交双曲线于点B1,过点B1作y轴的垂线交直线l于点A2,继续操作:过点A2作x轴的垂线交双曲线于点B2,过点B2作y轴的垂线交直线l于点A3,…,依次这样得到双曲线上的点B1,B2,B3,B4,…,Bn.记点A1的横坐标为2,则B2016的坐标为 .
查看答案和解析>>
科目:初中数学 来源:2016届山东省聊城市东昌府区中考一模数学试卷(解析版) 题型:解答题
如图,在一个18米高的楼顶上有一信号塔DC,李明同学为了测量信号塔的高度,在地面的A处测的信号塔下端D的仰角为30°,然后他正对塔的方向前进了18米到达地面的B处,又测得信号塔顶端C的仰角为60°,CD⊥AB与点E,E、B、A在一条直线上.请你帮李明同学计算出信号塔CD的高度(结果保留整数,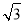 ≈1.7,
≈1.7,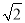 ≈1.4)
≈1.4)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com