练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    若反比例函数数学公式与二次函数y=ax2的图象的公共点在第三象限，则一次函数y=-ax-k的图象不经过


    1. A.
      第一象限
    2. B.
      第二象限
    3. C.
      第三象限
    4. D.
      第四象限
    B
    分析：根据公共点在第三象限确定出a、k的正负情况，再根据一次函数的性质解答．
    解答：∵y=与y=ax2的图象的公共点在第三象限，
    ∴a＜0，k＞0，
    ∴-a＞0，-k＜0，
    ∴y=-ax-k经过第一三象限，且与y轴的负半轴相交，
    ∴一次函数图象不经过第二象限．
    故选B．
    点评：本题考查了二次函数的性质，一次函数图象与系数的关系，反比例函数的性质，根据交点在第三象限确定出a、k的正负情况是解题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    （2012•静海县二模）已知二次函数y1=ax2+bx+c（a≠0）的图象经过三点（1，0），（-3，0），（0，-
    3
    2
    ）．
    （Ⅰ）求二次函数的解析式；
    （Ⅱ）若（Ⅰ）中的二次函数，当x取a，b（a≠b）时函数值相等，求x取a+b时的函数值；
    （Ⅲ）若反比例函数y2=
    k
    x
    （k＞0，x＞0）的图象与（Ⅰ）中的二次函数的图象在第一象限内的交点为A，点A的横坐标为x0满足2＜x0＜3，试求实数k的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2013•长沙）设a、b是任意两个不等实数，我们规定：满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间，表示为[a，b]．对于一个函数，如果它的自变量x与函数值y满足：当m≤x≤n时，有m≤y≤n，我们就称此函数是闭区间[m，n]上的“闭函数”．
    （1）反比例函数y=
    2013
    x
    是闭区间[1，2013]上的“闭函数”吗？请判断并说明理由；
    （2）若一次函数y=kx+b（k≠0）是闭区间[m，n]上的“闭函数”，求此函数的解析式；
    （3）若二次函数y=
    1
    5
    x2-
    4
    5
    x-
    7
    5
    是闭区间[a，b]上的“闭函数”，求实数a，b的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知二次函数y=ax2+bx+c（a≠0）自变量x与函数值y之间满足下列数量关系：
    x -4 -3 -2 -1 0 1 2 3 4 5 6
    y 24 15 8 3 0 -1 0 3 8 15  
    （1）观察表中数据，当x=6时，y的值是
     
    ；
    （2）这个二次函数与x轴的交点坐标是
     
    ；
    （3）代数式
    -b+
    		b2-4ac
    2a
    +
    -b-
    		b2-4ac
    2a
    +（a+b+c）（a-b+c）的值是
     
    ；
    （4）若s、t是两个不相等的实数，当s≤x≤t时，二次函数y=ax2+bx+c（a≠0）有最小值0和最大值24，那么经过点（s+1，t+1）的反比例函数解析式是
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    已知二次函数y1=ax2+bx+c（a≠0）的图象经过三点（1，0），（-3，0），（0，-数学公式）．
    （Ⅰ）求二次函数的解析式；
    （Ⅱ）若（Ⅰ）中的二次函数，当x取a，b（a≠b）时函数值相等，求x取a+b时的函数值；
    （Ⅲ）若反比例函数y2=数学公式（k＞0，x＞0）的图象与（Ⅰ）中的二次函数的图象在第一象限内的交点为A，点A的横坐标为x0满足2＜x0＜3，试求实数k的取值范围．

    查看答案和解析>>

    科目：初中数学 来源：2012年天津市静海县中考数学二模试卷（解析版） 题型：解答题

    已知二次函数y1=ax2+bx+c（a≠0）的图象经过三点（1，0），（-3，0），（0，-）．
    （Ⅰ）求二次函数的解析式；
    （Ⅱ）若（Ⅰ）中的二次函数，当x取a，b（a≠b）时函数值相等，求x取a+b时的函数值；
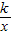    （Ⅲ）若反比例函数y2=（k＞0，x＞0）的图象与（Ⅰ）中的二次函数的图象在第一象限内的交点为A，点A的横坐标为x满足2＜x＜3，试求实数k的取值范围．

    查看答案和解析>>

    同步练习册答案