
【题目】对于一个函数,自变量x取a时,函数值y也等于a,我们称a为这个函数的不动点.如果二次函数y=x2+2x+c有两个相异的不动点x1、x2,且x1<1<x2,则c的取值范围是( )
A. c<﹣3B. c<﹣2C. c<![]() D. c<1
D. c<1
【答案】B
【解析】
由题意知二次函数y=x2+2x+c有两个相异的不动点x1、x2,由此可知方程x2+x+c=0有两个不相等的实数根,即△=1-4c>0,再由题意可得函数y= x2+x+c=0在x=1时,函数值小于0,即1+1+c<0,由此可得关于c的不等式组,解不等式组即可求得答案.
由题意知二次函数y=x2+2x+c有两个相异的不动点x1、x2,
所以x1、x2是方程x2+2x+c=x的两个不相等的实数根,
整理,得:x2+x+c=0,
所以△=1-4c>0,
又x2+x+c=0的两个不相等实数根为x1、x2,x1<1<x2,
所以函数y= x2+x+c=0在x=1时,函数值小于0,
即1+1+c<0,
综上则![]() ,
,
解得c<﹣2,
故选B.


科目:初中数学 来源: 题型:
【题目】为了研究一种新药的疗效,选100名患者随机分成两组,每组各50名,一组服药,另一组不服药,12周后,记录了两组患者的生理指标![]() 和
和![]() 的数据,并制成下图,其中“*”表示服药者,“+”表示未服药者;
的数据,并制成下图,其中“*”表示服药者,“+”表示未服药者;
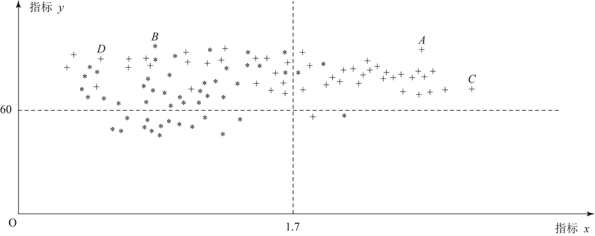
同时记录了服药患者在4周、8周、12周后的指标z的改善情况,并绘制成条形统计图.

根据以上信息,回答下列问题:
(1)从服药的50名患者中随机选出一人,求此人指标![]() 的值大于1.7的概率;
的值大于1.7的概率;
(2)设这100名患者中服药者指标![]() 数据的方差为
数据的方差为![]() ,未服药者指标
,未服药者指标![]() 数据的方差为
数据的方差为![]() ,则
,则![]()
![]() ;(填“>”、“=”或“<” )
;(填“>”、“=”或“<” )
(3)对于指标z的改善情况,下列推断合理的是 .
①服药4周后,超过一半的患者指标z没有改善,说明此药对指标z没有太大作用;
②在服药的12周内,随着服药时间的增长,对指标z的改善效果越来越明显.
查看答案和解析>>
科目:初中数学 来源: 题型:
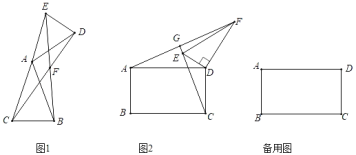
【题目】(1)如图1,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=30°,连接CD,BE交于点F.![]() = ;∠BFD= ;
= ;∠BFD= ;
(2)如图2,在矩形ABCD和△DEF中,AB=![]() AD,∠EDF=90°,∠DEF=60°,连接AF交CE的延长线于点G.求
AD,∠EDF=90°,∠DEF=60°,连接AF交CE的延长线于点G.求![]() 的值及∠AGC的度数,并说明理由.
的值及∠AGC的度数,并说明理由.
(3)在(2)的条件下,将△DEF绕点D在平面内旋转,AF,CE所在直线交于点P,若DE=1,AD=![]() ,求出当点P与点E重合时AF的长.
,求出当点P与点E重合时AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】开学前夕,某文具店准备购进A、B两种品牌的文具袋进行销售,若购进A品牌文具袋和B品牌文具袋各5个共花费125元,购进A品牌文具袋3个和B品牌文具袋各4个共花费90元.
(1)求购进A品牌文具袋和B品牌文具袋的单价;
(2)若该文具店购进了A,B两种品牌的文具袋共100个,其中A品牌文具袋售价为12元,B品牌文具袋售价为23元,设购进A品牌文具袋x个,获得总利润为y元.
①求y关于x的函数关系式;
②要使销售文具袋的利润最大,且所获利润不超过进货价格的40%,请你帮该文具店设计一个进货方案,并求出其所获利润的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某县建档立卡贫困户对精准扶贫政策落实的满意度,现从全县建档立卡贫困户中随机抽取了部分贫困户进行了调查(把调查结果分为四个等级:A级:非常满意;B级:满意;C级:基本满意;D级:不满意),并将调查结果绘制成如下两幅不完整的统计图.请根据统计图中的信息解决下列问题:
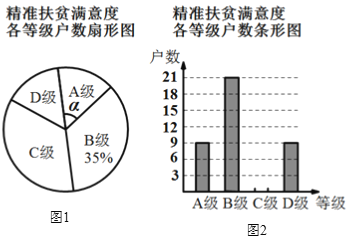
(1)本次抽样调查测试的建档立卡贫困户的总户数______.
(2)图1中,∠α的度数是______,并把图2条形统计图补充完整.
(3)某县建档立卡贫困户有10000户,如果全部参加这次满意度调查,请估计非常满意的人数约为多少户?
(4)调查人员想从5户建档立卡贫困户(分别记为![]() )中随机选取两户,调查他们对精准扶贫政策落实的满意度,请用列表或画树状图的方法求出选中贫困户
)中随机选取两户,调查他们对精准扶贫政策落实的满意度,请用列表或画树状图的方法求出选中贫困户![]() 的概率.
的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解七、八年级学生一分钟跳绳情况,从这两个年级随机抽取![]() 名学生进行测试,并对测试成绩(一分钟跳绳次数)进行整理、描述和分析,下面给出了部分信息:
名学生进行测试,并对测试成绩(一分钟跳绳次数)进行整理、描述和分析,下面给出了部分信息:
七年级学生一分钟跳绳成绩频数分布直方图
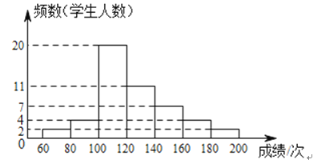
七、八年级学生一分钟跳绳成绩分析表

七年级学生一分钟跳绳成绩(数据分![]() 组:
组:![]() )在
)在![]() 这一组的是:
这一组的是:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
根据以上信息,回答下列问题:
![]() 表中
表中![]() ;
;
![]() 在这次测试中,七年级甲同学的成绩
在这次测试中,七年级甲同学的成绩![]() 次,八年级乙同学的成绩
次,八年级乙同学的成绩![]() ,他们的测试成绩,在各自年级所抽取的
,他们的测试成绩,在各自年级所抽取的![]() 名同学中,排名更靠前的是 (填“甲”或“乙”),理由是 .
名同学中,排名更靠前的是 (填“甲”或“乙”),理由是 .
![]() 该校七年级共有
该校七年级共有![]() 名学生,估计一分钟跳绳不低于
名学生,估计一分钟跳绳不低于![]() 次的有多少人?
次的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
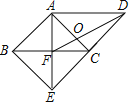
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,过点
,过点![]() 作边
作边![]() 的垂线
的垂线![]() 交
交![]() 的延长线于点
的延长线于点![]() ,点
,点![]() 是垂足,连接
是垂足,连接![]() 、
、![]() ,
,![]() 交
交![]() 于点
于点![]() .则下列结论:①四边形
.则下列结论:①四边形![]() 是正方形;②
是正方形;②![]() ;③
;③![]() ;④
;④![]() ,正确的个数是( )
,正确的个数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接2022年冬奥会,鼓励更多的大学生参与到志愿服务中,甲、乙两所学校组织了志愿服务团队选拔活动,经过初选,两所学校各有300名学生进入综合素质展示环节,为了了解这些学生的整体情况,从两校进入综合素质展示环节的学生中分别随机抽取了50名学生的综合素质展示成绩(百分制),并对数据(成绩)进行整理、描述和分析,下面给出了部分信息.
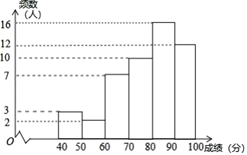
a.甲学校学生成绩的频数分布直方图如图(数据分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ).
).
b.甲学校学生成绩在![]() 这一组是:
这一组是:
80 80 81 81.5 82 83 83 84
85 86 86.5 87 88 88.5 89 89
c.乙学校学生成绩的平均数、中位数、众数、优秀率(85分及以上为优秀)如下:
平均数 | 中位数 | 众数 | 优秀率 |
83.3 | 84 | 78 | 46% |
根据以上信息,回答下列问题:
(1)甲学校学生![]() ,乙学校学生
,乙学校学生![]() 的综合素质展示成绩同为82分,这两人在本校学生中综合素质展示排名更靠前的是________(填“
的综合素质展示成绩同为82分,这两人在本校学生中综合素质展示排名更靠前的是________(填“![]() ”或“
”或“![]() ”);
”);
(2)根据上述信息,推断________学校综合素质展示的水平更高,理由为:__________________________
(至少从两个不同的角度说明推断的合理性).
(3)若每所学校综合素质展示的前120名学生将被选入志愿服务团队,预估甲学校分数至少达到________分的学生才可以入选.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com