
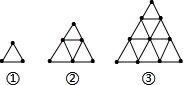
 探索规律并填空
探索规律并填空| 图形编号 | ① | ② | ③ | ④ |
| 大三角形周长的火柴棒根数 | 3 | 6 | 9 | 12 |
| 小三角形个数 | 1 | 4 | 9 | 16 |
分析 (1)连续整数的和等于首尾两数的和乘以数字的个数的一半,据此可得;图形中,大三角形周长的火柴棒根数为序数的3倍,小三角形的个数是序数的平方,据此可完善表格,解决问题;
(2)根据(1)中所得规律解答即可.
解答 解:(1)1+2+3+…+20=$\frac{20×(1+20)}{2}$=210,1+2+3+…+n=$\frac{n(n+1)}{2}$,
| 图形编号 | ① | ② | ③ | ④ |
| 大三角形周长的火柴棒根数 | 3 | 6 | 9 | 12 |
| 小三角形个数 | 1 | 4 | 9 | 16 |
点评 此题主要考查了图形的变化类问题,要熟练掌握,解答此类问题的关键是首先应找出图形哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.探寻规律要认真观察、仔细思考,善用联想来解决这类问题.


科目:初中数学 来源: 题型:填空题
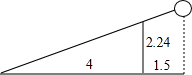 已知女排赛场标准球网的高度是2.24米,在2016年奥运会女排比赛中,某队球员在一次扣球时,球恰好擦网而过(击球擦网落地过程为直线),落在对方场地距离球网4米的位置上,此时该运动员距离球网1.5米,则该运动员击球的高度是3.08米.
已知女排赛场标准球网的高度是2.24米,在2016年奥运会女排比赛中,某队球员在一次扣球时,球恰好擦网而过(击球擦网落地过程为直线),落在对方场地距离球网4米的位置上,此时该运动员距离球网1.5米,则该运动员击球的高度是3.08米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4x2y+xy+3xy2=xy(4x+3y) | B. | $\frac{1}{4}$a2+ab+b2=$\frac{1}{4}$(a+2b)2 | ||
| C. | m2+4=(m+2)2 | D. | 若x2-x+42=(x+a)(x+b),则a,b异号 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-3)2的算术平方根是3 | B. | $\sqrt{225}$的平方根是±15 | ||
| C. | 当x=0或2时,x$\sqrt{x-2}$=0 | D. | $\frac{\sqrt{3}}{2}$是分数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com