
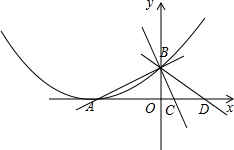
���� ���������A����B�͵�C�����꣬Ȼ�����D������Ϊ��a��0�������á�BCD=��ABD����BDC=��ADB֤����BCD�ס�ABD���ɵ�$\frac{BD}{AD}=\frac{BC}{AB}$���г�a�ķ��̣����a��ֵ�������õ�D������꣬���������B��D�����һ�κ�������ʽ��
���  �⣺�������⻭ͼ���ң�
�⣺�������⻭ͼ���ң�
��y=$\frac{\sqrt{2}}{9}$x2+$\frac{2\sqrt{2}}{3}$x+$\sqrt{2}$=0��
���x=-3��
����A������-3��0����
��x=0��y=$\sqrt{2}$��
����B���꣨0��$\sqrt{2}$����
��һ�κ���y=-$\sqrt{2}$x+bͼ��B�㣬
��b=$\sqrt{2}$��
��C��������1��0����
���D��������a��0����
�ߡ�BCD=��ABD����BDC=��ADB��
���BCD�ס�ABD��
��$\frac{BD}{AD}=\frac{BC}{AB}$��
��$\frac{\sqrt{{a}^{2}+2}}{a+3}=\frac{\sqrt{3}}{\sqrt{11}}$��
��a=$\frac{5}{2}$��a=-$\frac{1}{4}$��
���D������$\frac{5}{2}$��0����-$\frac{1}{4}$��0����
��ֱ��BD�Ľ���ʽΪy=kx+$\sqrt{2}$��
����D����Ϊ��$\frac{5}{2}$��0��ʱ��
k=-$\frac{2\sqrt{2}}{5}$��
ֱ��BD�Ľ���ʽΪy=-$\frac{2\sqrt{2}}{5}$x+$\sqrt{2}$��
����D������-$\frac{1}{4}$��0����
k=4$\sqrt{2}$��
ֱ��BD�Ľ���ʽΪy=4$\sqrt{2}$x+$\sqrt{2}$��
�ʴ�Ϊy=-$\frac{2\sqrt{2}}{5}$x+$\sqrt{2}$��y=4$\sqrt{2}$x+$\sqrt{2}$��
���� ������Ҫ��������������x�ύ���֪ʶ�������Ĺؼ����ɡ�BCD�ס�ABD�õ���D�����꣬������һ�����Ѷȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5.29��10-8cm | B�� | 5.29��10-9cm | C�� | 0.529��10-8cm | D�� | 52.9��10-10cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{600}{x-50}$=$\frac{450}{x}$ | B�� | $\frac{600}{x}$=$\frac{450}{x+50}$ | C�� | $\frac{600}{x+50}$=$\frac{450}{x}$ | D�� | $\frac{600}{x}$=$\frac{450}{x-50}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
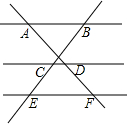 ��ͼ��AB��CD��EF��AD=4��BC=DF=3����BE�ij�Ϊ$\frac{21}{4}$��
��ͼ��AB��CD��EF��AD=4��BC=DF=3����BE�ij�Ϊ$\frac{21}{4}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com