练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知:如图,△ABC中,点O是AC上的一动点,过点O作直线MN∥AB,设MN交∠BCA的平分线于点E,交∠BCA的外角∠ACG的平分线于点F连接AE、AF.

    (1)求证:∠ECF=90°；

    (2)当点O运动到何处时,四边形AECF是矩形?请说明理由；

    (3)在(2)的条件下,△ABC应该满足条件:______________，就能使矩形AECF变为正方形。(直接添加条件,无需证明)

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：山东省2019届九年级上学期第一次月考数学试卷 题型：填空题

    如图所示，在同一平面直角坐标系中，作出①y=﹣3x2，②y=﹣，③y=﹣x2的图象，则从里到外的三条抛物线对应的函数依次是______（填序号）

    查看答案和解析>>

    科目：初中数学 来源：北师大新版数学九年级上学期《6.1反比例函数》同步练习 题型：单选题

    下列函数中是反比例函数的是（　　）

    A. y=x﹣1 B. y= C. y= D. =1

    查看答案和解析>>

    科目：初中数学 来源：江苏省无锡市2019届九年级10月月考数学试卷 题型：填空题

    若方程的两根为、，则·的值为__________．

    查看答案和解析>>

    科目：初中数学 来源：江苏省无锡市2019届九年级10月月考数学试卷 题型：单选题

    若关于的一元二次方程有实数根, 则实数的取值范围是 ( )

    A. ≥－1 B. ＞－1 C. ≠0 D. ≥－1且≠0

    查看答案和解析>>

    科目：初中数学 来源：陕西省西安市2018届九年级上第一次月考数学试卷 题型：解答题

    如图，要利用一面墙（墙长为25米）建羊圈，用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈，求羊圈的边长AB，BC各为多少米？

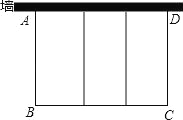
    查看答案和解析>>

    科目：初中数学 来源：河南省洛阳市2019届九年级第一学期月考数学 题型：解答题

    用适当的方法解下列一元二次方程：

    (1)2x2 -1=7; (2)x2 -5x+6=0;

    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市2019届九年级（上）第一次月考数学试卷 题型：解答题

    随着人们环保意识的不断增强，我市家庭电动自行车的拥有量逐年增加．据统计，某小区2014年底拥有家庭电动自行车125辆，2016年底家庭电动自行车的拥有量达到180辆．

    （1）若该小区2014年底到2017年底家庭电动自行车拥有量的年平均增长率相同，则该小区到2017年底电动自行车将达到多少辆？

    （2）为了缓解停车矛盾，该小区决定投资3万元再建若干个停车位，据测算，建造费用分别为室内车位1000元/个，露天车位200元/个．考虑到实际因素，计划露天车位的数量不少于室内车位的2倍，但不超过室内车位的2.5倍，则该小区最多可建两种车位各多少个？试写出所有可能的方案．

    查看答案和解析>>

    科目：初中数学 来源：江苏省无锡市2019届九年级10月月考数学试卷 题型：填空题

    若方程的两根分别是，则=___．

    查看答案和解析>>

    同步练习册答案