
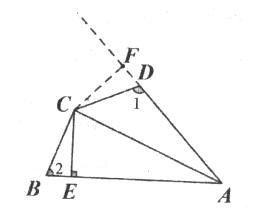
【题目】如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于E,且AE=![]() (AD+AB).请你猜想∠1和∠2有什么数量关系?并证明你的猜想.
(AD+AB).请你猜想∠1和∠2有什么数量关系?并证明你的猜想.
解:猜想: .
证明:

【答案】∠1+∠2=180°
【解析】
延长AD过C作CF垂直AD于F,由条件可证△AFC≌△AEC,得到CF=CE.再由条件![]() ,可证BE=DF,所以△CDF≌△CEB,由全等的性质可得∠ABC=∠CDF,问题可得解.
,可证BE=DF,所以△CDF≌△CEB,由全等的性质可得∠ABC=∠CDF,问题可得解.
猜想:∠1+∠2=180°
证明:过C点作CF⊥AD延长线于点F,
∵CE⊥AB,AC平分∠DAB,
∴CB=CF,
∠CEB=∠CFD=90°,
在Rt△CEA和Rt△CFA中
∵![]()
∴Rt△CEA≌Rt△CFA(HL),
∴AE=AF,
∵![]() ,
,
AE+AF=AF-FD+AE+BE,
∴FD=BE,
在△CEB和△CFD中
∵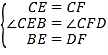
∴△CEB≌△CFD(SAS),
∴∠2=∠CDF,
∵∠CDF+∠1=180°,
∴∠1+∠2=180°.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】最近,“校园安全”受到全社会的广泛关注,重庆八中对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如下两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)扇形统计图中“基本了解”部分所对应扇形的圆心角为度;请补全条形统计图;
(2)若达到“了解”程度的人中有1名男生2名女生,达到“不了解”的程度的人中有1名男生和1名女生,若分别从达到“了解”程度和“不了解”的人中分别抽取1人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1名男生和1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校园内有一块菱形的空地ABCD,为了美化环境,现要进行绿化,计划在中间建设一个面积为S的矩形绿地EFGH,其中,点E、F、G、H分别在菱形的四条边上,AB=a米,BE=BF=DG=DH=x米,∠A=60° 
(1)求S关于x的函数关系式,并直接写出自变量x的取值范围;
(2)若a=100,求S的最大值,并求出此时x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作BE的平行线与线段ED的延长线交于点F,连接AE,CF.
(1)求证:AF=CE;
(2)若AC=EF,试判断四边形AFCE是什么样的四边形,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高速公路的同一侧有A、B两城镇,如图,它们到高速公路所在直线MN的距离分别为AA′=2 km,BB′=4 km,A′B′=8 km.要在高速公路上A′、B′之间建一个出口P,使A、B两城镇到P的距离之和最小.求这个最短距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两同学从A地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系图象如图所示,根据图中提供的信息,有下列说法:

(1)他们都行驶了18千米;
(2)甲在途中停留了0.5小时;
(3)乙比甲晚出发了0.5小时;
(4)相遇后,甲的速度小于乙的速度;
(5)甲、乙两人同时到达目的地
其中符合图象描述的说法有( )
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为4的正方形ABCD内接于点O,点E是 ![]() 上的一动点(不与A、B重合),点F是
上的一动点(不与A、B重合),点F是 ![]() 上的一点,连接OE、OF,分别与AB、BC交于点G,H,且∠EOF=90°,有以下结论: ①
上的一点,连接OE、OF,分别与AB、BC交于点G,H,且∠EOF=90°,有以下结论: ① ![]() =
= ![]() ;
;
②△OGH是等腰三角形;
③四边形OGBH的面积随着点E位置的变化而变化;
④△GBH周长的最小值为4+ ![]() .
.
其中正确的是(把你认为正确结论的序号都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
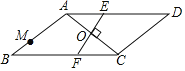
【题目】如图,在ABCD中,∠B=30°,AB=AC,O是两条对角线的交点,过点O作AC的垂线分别交边AD,BC于点E,F;点M是边AB的一个三等分点,则△AOE与△BMF的面积比为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com