
 如图,AB是⊙O的直径,且AB=10,弦MN的长为8,若弦MN的两端在圆周上滑动,始终与AB相交.记点A,B到MN的距离为h1,h2.则|h1-h2|等于( )
如图,AB是⊙O的直径,且AB=10,弦MN的长为8,若弦MN的两端在圆周上滑动,始终与AB相交.记点A,B到MN的距离为h1,h2.则|h1-h2|等于( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
分析 设AB、NM交于H,做OD⊥MN于D,连接OM,利用垂径定理及勾股定理可求出OD,再推△AFH∽△ODH∽△BEH,然后就可利用OH表示BE、AF,从而可求出答案.
解答 解:设AB、NM交于H,做OD⊥MN于D,连接OM,
∵AB是⊙O的直径,且AB=10,弦MN的长为8,
∴DN=DM=4,OD=3,
∵BE⊥MN,AF⊥MN,OD⊥MN,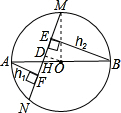
∴BE∥OD∥AF,
∴△AFH∽△ODH∽△BEH,
∴AF:OD=AF:3=(5-OH):OH,
即$\frac{AF}{3}=\frac{5-OH}{OH}$,$\frac{BE}{OD}=\frac{HB}{OH}=\frac{5+OH}{OH}$,
即$\frac{BE}{3}=\frac{5+OH}{OH}$,
∴$\frac{1}{3}$(AF-BE)=-2,
∴|h1-h2|=|AF-BE|=6.
故选B.
点评 本题考查了垂径定理,解答本题需仔细分析图形,利用垂径定理和相似三角形的性质即可解决问题.对于一个圆和一条直线来说如果一条直线具备下列,①经过圆心,②垂直于弦,③平分弦(弦不是直径),④平分弦所对的优弧,⑤平分弦所对的劣弧,五个条件中的任何两个,那么也就具备其他三个.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a>0,b>0 | B. | a<0,b<0 | C. | a>0,b<0 | D. | a<0,b>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在四边形ABCD中,AD∥BC,AC,BD交于点O,过点O作EF∥AD交AB于点E,F,若AE=2,BE=5,OD=3,则BD长为( )
如图,在四边形ABCD中,AD∥BC,AC,BD交于点O,过点O作EF∥AD交AB于点E,F,若AE=2,BE=5,OD=3,则BD长为( )| A. | 6 | B. | $\frac{15}{2}$ | C. | $\frac{21}{2}$ | D. | $\frac{10}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com