
如图,在平面直角坐标系中,矩形OEFG的顶点F的坐标为(4,2),将矩形OEFG绕点O逆时针旋转,使点F落在y轴上,得到矩形OMNP,OM与GF相交于点A.若经过点A的反比例函数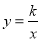 (x>0)的图象交EF于点B,则点B的坐标为____________.
(x>0)的图象交EF于点B,则点B的坐标为____________.

(4,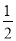 ).
).
【解析】
试题分析:根据旋转的性质得到∠P=∠POM=∠OGF=90°,再根据等角的余角相等可得∠PNO=∠GOA,然后根据相似三角形的判定方法即可得到△OGA∽△NPO;由E点坐标为(4,0),G点坐标为(0,2)得到OE=4,OG=2,则OP=OG=2,PN=GF=OE=4,由于△OGA∽△NPO,则OG:NP=GA:OP,即2:4=GA:2,可求得GA=1,可得到A点坐标为(1,2),然后利用待定系数法即可得到过点A的反比例函数解析式,再利用B点的横坐标为4和B点在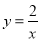 得到B点坐标即可.
得到B点坐标即可.
试题解析:∵矩形OEFG绕点O逆时针旋转,使点F落在y轴的点N处,得到矩形OMNP,
∴∠P=∠POM=∠OGF=90°,
∴∠PON+∠PNO=90°,∠GOA+∠PON=90°,
∴∠PNO=∠GOA,
∴△OGA∽△NPO;
∵E点坐标为(4,0),G点坐标为(0,2),
∴OE=4,OG=2,
∴OP=OG=2,PN=GF=OE=4,
∵△OGA∽△NPO,
∴OG:NP=GA:OP,即2:4=GA:2,
∴GA=1,
∴A点坐标为(1,2),
设过点A的反比例函数解析式为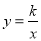
把A(1,2)代入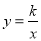 得k=1×2=2,
得k=1×2=2,
∴过点A的反比例函数解析式为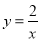 ;
;
把x=4代入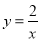 中得y=
中得y=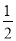 ,
,
∴B点坐标为(4,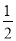 ).
).
考点:反比例函数综合题.


科目:初中数学 来源:2013-2014学年重庆市万州区岩口复兴学校九年级下学期期中命题四数学试卷(解析版) 题型:选择题
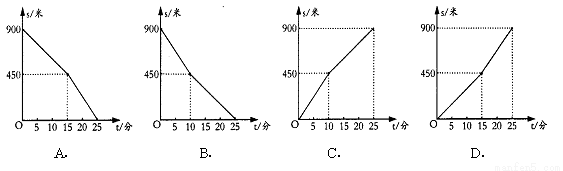
小明每天从家去学校上学行走的路程为900米,某天他从家去上学时以每分30米的速度行走了450米,为了不迟到,他加快了速度,以每分45米的速度行走完剩下的路程,那么小明行走过的路程S(米)与他行走的时间t(分)之间的函数关系用图象表示正确的是 ( )
查看答案和解析>>
科目:初中数学 来源:2013-2014学年重庆市九年级3月月考数学试卷(解析版) 题型:解答题
我市高新技术开发区的某公司,用480万元购得某种产品的生产技术后,并进一步投入资金1520万元购买生产设备,进行该产品的生产加工,已知生产这种产品每件还需成本费40元.经过市场调研发现:该产品的销售单价,需定在100元到300元之间较为合理.当销售单价定为100元时,年销售量为20万件;当销售单价超过100元,但不超过200元时,每件新产品的销售价格每增加10元,年销售量将减少0.8万件;当销售单价超过200元,但不超过300元时,每件产品的销售价格每增加10元,年销售量将减少1万件.设销售单价为x(元),年销售量为y(万件),年获利为w(万元).(年获利=年销售额-生产成本-投资成本)
(1)直接写出y与x之间的函数关系式;
(2)求第一年的年获利w与x间的函数关系式,并说明投资的第一年,该公司是盈利还是亏损?若盈利,最大利润是多少?若亏损,最少亏损是多少?
(3)若该公司希望到第二年底,除去第一年的最大盈利(或最小亏损)后,两年的总盈利不低于1842元,请你确定此时销售单价的范围.在此情况下,要使产品销售量最大,销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源:2013-2014学年重庆市九年级3月月考数学试卷(解析版) 题型:填空题
地球到月球的距离约为380000公里,将数380000用科学记数法表示为________公里
查看答案和解析>>
科目:初中数学 来源:2013-2014学年重庆市九年级3月月考数学试卷(解析版) 题型:选择题
如图,AP、BP分别切⊙O于点A、B,∠P=60°,点C是圆上一动点,则∠C度数为( )
A.60° C.40° D.72° D、60°或120°

查看答案和解析>>
科目:初中数学 来源:2013-2014学年辽宁省丹东市九年级第一次模拟考试数学试卷(解析版) 题型:解答题
如图,抛物线:y=ax2+bx+4与x轴交于点A(-2,0)和B(4,0)、与y轴交于点C.
(1)求抛物线的解析式;
(2)T是抛物线对称轴上的一点,且△ACT是以AC为底的等腰三角形,求点T的坐标;
(3)点M、Q分别从点A、B以每秒1个单位长度的速度沿x轴同时出发相向而行.当点M原点时,点Q立刻掉头并以每秒个单位长度的速度向点B方向移动,当点M到达抛物线的对称轴时,两点停止运动.过点M的直线l⊥轴,交AC或BC于点P.求点M的运动时间t(秒)与△APQ的面积S的函数关系式,并求出S的最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com