Question

13．我们知道，三角形三个内角平分线的交点叫做三角形的内心，已知点I为△ABC的内心．

（1）如图1，连接AI并延长交BC于点D，若AB=AC=3，BC=2，求ID的长；
（2）如图2，过点I作直线交AB于点M，交AC于点N．
①若MN⊥AI，求证：MI²=BM•CN；
②如图3，AI交BC于点D，若∠BAC=60°，AI=4，求$\frac{1}{AM}$+$\frac{1}{AN}$的值．

Answer 1

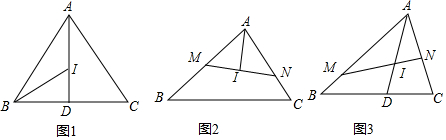
分析 （1）如图1中，作IE⊥AB于E．设ID=x．由△BEI≌△BDI，可得ID=IE=x，BD=BE=1，AE=2，在Rt△AEI中，根据AE²+EI²=AI²，可得2²+x²=（2$\sqrt{2}$-x）²，解方程即可；
（2）如图2中，连接BI、CI．首先证明△AMI≌△ANI（ASA），再证明△BMI∽△INC，可得$\frac{BM}{NI}$=$\frac{NI}{NC}$，推出NI²=BM•CN，由此即可解决问题；
（3）过点N作NG∥AD交MA的延长线于G．由∠ANG=∠AGN=30°，推出AN=AG，NG=$\sqrt{3}$AN，由AI∥NG，推出$\frac{AM}{MG}$=$\frac{AI}{NG}$，可得$\frac{AM}{AM+AN}$=$\frac{4}{\sqrt{3}AN}$，即可推出$\frac{1}{AM}$+$\frac{1}{AN}$=$\frac{\sqrt{3}}{4}$；

解答 解：（1）如图1中，作IE⊥AB于E．设ID=x．

∵AB=AC=3，AI平分∠BAC，
∴AD⊥BC，BD=CD=1，
在Rt△ABD中，AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{{3}^{2}-{1}^{2}}$=2$\sqrt{2}$，
∵∠EBI=∠DBI，∠BEI=∠BDI=90°，BI=BI，
∴△BEI≌△BDI，
∴ID=IE=x，BD=BE=1，AE=2，
在Rt△AEI中，∵AE²+EI²=AI²，
∴2²+x²=（2$\sqrt{2}$-x）²，
∴x=$\frac{\sqrt{2}}{2}$，
∴ID=$\frac{\sqrt{2}}{2}$．

（2）如图2中，连接BI、CI．

∵I是内心，
∴∠MAI=∠NAI，
∵AI⊥MN，
∴∠AIM=∠AIN=90°，
∵AI=AI，
∴△AMI≌△ANI（ASA），
∴∠AMN=∠ANM，
∴∠BMI=∠CNI，
设∠BAI=∠CAI=α，∠ACI=∠BCI=β，
∴∠NIC=90°-α-β，
∵∠ABC=180°-2α-2β，
∴∠MBI=90°-α-β，
∴∠MBI=∠NIC，
∴△BMI∽△INC，
∴$\frac{BM}{NI}$=$\frac{NI}{NC}$，
∴NI²=BM•CN，
∵NI=MI，
∴MI²=BM•CN．

（3）过点N作NG∥AD交MA的延长线于G．

∴∠ANG=∠AGN=30°，
∴AN=AG，NG=$\sqrt{3}$AN，
∵AI∥NG，
∴$\frac{AM}{MG}$=$\frac{AI}{NG}$，
∴$\frac{AM}{AM+AN}$=$\frac{4}{\sqrt{3}AN}$，
∴$\frac{1}{AM}$+$\frac{1}{AN}$=$\frac{\sqrt{3}}{4}$．

点评 本题考查三角形综合题、相似三角形的判定和性质、三角形的内心、角平分线的性质、平行线的性质等知识，解题的关键是学会添加常用辅助线，灵活运用所学知识解决问题，属于中考压轴题．