
【题目】如图,一次函数y1=kx+b的图象与反比例函数y2=![]() 的图象相交于A,B两点,直线AB与x轴相交于点C,点B的坐标为(﹣6,m),线段OA=5,E为x轴正半轴上一点,且cos∠AOE=
的图象相交于A,B两点,直线AB与x轴相交于点C,点B的坐标为(﹣6,m),线段OA=5,E为x轴正半轴上一点,且cos∠AOE=![]() .
.
(1)求反比例函数的解析式;
(2)求证:S△AOC=2S△BOC;
(3)直接写出当y1>y2时,x的取值范围.
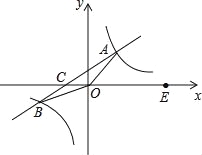
【答案】(1)反比例函数解析式为![]() ;
;
(2)证明见解析
(3)当y1>y2时,x的取值范围为﹣6<x<0或x>3.

【解析】
试题分析:(1)通过解直角三角形求出点A的坐标,进而得出反比例函数解析式;
(2)先根据反比例函数解析式求得点B的坐标,再由点A、B的坐标利用待定系数法求出直线AB的解析式,进而得到OC的长,最后计算△AOC和△BOC的面积并得出结论;
(3)结合两函数图象,找出反比例函数图象在一次函数图象下方时x的取值范围即可.
试题解析:过点A作AD⊥x轴于点D,∵cos∠AOE=![]() =
=![]() ,∴OD=3
,∴OD=3
∴AD=![]() =4,∴A(3,4),将点A的坐标代入反比例函数y2=
=4,∴A(3,4),将点A的坐标代入反比例函数y2=![]() 得,a=12
得,a=12
∴反比例函数解析式为![]() ;
;
(2)将点B(﹣6,m)代入反比例函数![]() 得,m=﹣2,∴B(﹣6,﹣2)
得,m=﹣2,∴B(﹣6,﹣2)
将A(3,4),B(﹣6,m)代入一次函数y1=kx+b,得
![]() ,解得
,解得![]()
∴一次函数解析式为![]()
当y=0时,![]() ,即x=﹣3,∴C(﹣3,0),∴OC=3
,即x=﹣3,∴C(﹣3,0),∴OC=3
∴△AOC的面积=![]() ×3×4=6
×3×4=6
△BOC的面积=![]() ×3×2=3
×3×2=3
∴S△AOC=2S△BOC;
(3)当y1>y2时,x的取值范围为﹣6<x<0或x>3.



 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿DE,EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=98°,则∠C的度数为( ) 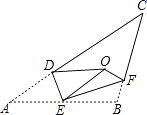
A.40°
B.41°
C.42°
D.43°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题4分)把下列各数分别填入相应的集合内:
-2.5,0,-0.5252252225…(每两个5之间依次增加1个2),100%,-(-2),![]() ,
,![]()
(1)正数集合:{ …};
(2)负分数集合:{ …};
(3)整数集合:{ …};
(4)无理数集合:{ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
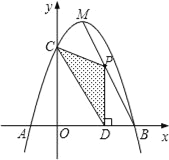
【题目】如图,抛物线y=﹣x2+bx+c与x轴相交于A、B两点,与y轴相交于点C,且点B与点C的坐标分别为B(3,0).C(0,3),点M是抛物线的顶点.
(1)求二次函数的关系式;
(2)点P为线段MB上一个动点,过点P作PD⊥x轴于点D.若OD=m,△PCD的面积为S,试判断S有最大值或最小值?并说明理由;
(3)在MB上是否存在点P,使△PCD为直角三角形?如果存在,请求出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,设一动点自P0(1,0)处向上运动1个单位长度至P1(1,1),然后向左运动2个单位至P2处,再向下运动3个单位至P3处,再向右运动4个单位至P4处,再向上运动5个单位至P5处,…如此继续运动下去,设Pn(xn , yn),n=1,2,3,…则x1+x2+…+x99+x100=( ) 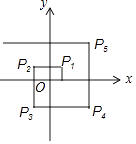
A.0
B.﹣49
C.50
D.﹣50
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com