解:(1)设长为xm,宽为(50-x)m,则S=x•(50-x)=-(x-25)
2+625,所以当每条边长为25m时,才能使长方形鸡场的面积最大;
(2)正五边形鸡场面积更大;
对于事实2,我们给出下述证明:
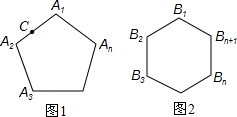
如图1、2,设正n边形A
1A
2A
n与正(n+1)边形A
1A
2A
n+1的周长相等,下面我们证明
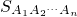
<
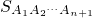
.在边A
1A
2上任取一点(异于点A
1、A
2),这样我们可以把A
1A
2A
n看成是(n+1)边形A
1CA
2A
n,但它显然不是正(n+1)边形,它的周长与正(n+1)边形A
1A
2A
n+1的周长相等,根据事实1,
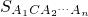
<
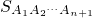
,即
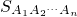
<
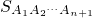
.
所以,等周长n边形的面积,当边数n越大时,其面积也越大;
(3)在周长相同的情况下,曲线围成正多边形面积较大;
正多边形的边数越大,图形越接近于圆,面积也越大,当边数无限增大时,正多边形无限地接近于圆,面积越来越接近于一个固定的值,这个值就是所围成的圆的面积;
(4)他讲的有道理.
设宽为xm,长为(100-2x)m,
则S=x•(100-2x)=-2(x-25)
2+1250,
所以当长为宽的2倍时,才能使长方形鸡场的面积最大.
有更好的方法:
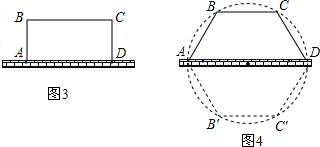
如图4,如果将图1中的点A、D分别向外移动.
那么ABCD仍然是四边形,而将四边形沿墙反射过来,这样就得到一个新的封闭六边形BCDC′B′A,它的周长等于原篱笆长度的两倍.
所以当六边形BCDC′B′A为正六边形,即AB=BC=CD,且∠BAD=∠CDA=60°,∠ABC=∠DCB=120°时,六边形BCDC′B′A的面积最大.
因而其一半即四边形ABCD的面积也最大.由于周长相等,
因此图4中正六边形BCDC′B′A的面积大于图3中正方形BCC′B′的面积,
所以图4中四边形ABCD的面积大于图3中四边形ABCD的面积.
分析:(1)设一边的长为x,用它表示另一边及面积,运用函数性质求解;
(2)、(3)可运用割圆术的思路,在某一个多边形的基础上把一边分成两边,细化下去便是圆;
(4)由(1)知小明讲的有道理.
点评:此题检测学生理解知识和运用知识的能力,考查学生的自主学习能力,因为理论性较强,所以宜作竞赛题使用.



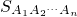 <
<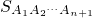 .在边A1A2上任取一点(异于点A1、A2),这样我们可以把A1A2An看成是(n+1)边形A1CA2An,但它显然不是正(n+1)边形,它的周长与正(n+1)边形A1A2An+1的周长相等,根据事实1,
.在边A1A2上任取一点(异于点A1、A2),这样我们可以把A1A2An看成是(n+1)边形A1CA2An,但它显然不是正(n+1)边形,它的周长与正(n+1)边形A1A2An+1的周长相等,根据事实1,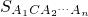 <
<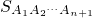 ,即
,即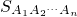 <
<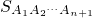 .
.



