
分析 (1)根据有理数的混合运算的运算方法,求出算式的值是多少即可.
(2)应用乘法分配律,求出算式的值是多少即可.
解答 解:(1)(+12)-(-17)+(-7)-(+21)
=12+17-7-21
=1
(2)(-$\frac{3}{4}$+$\frac{5}{3}$-$\frac{7}{12}$)÷$\frac{1}{36}$
=(-$\frac{3}{4}$)×36+$\frac{5}{3}$×36-$\frac{7}{12}$×36
=-27+60-21
=12
点评 此题主要考查了有理数的混合运算,要熟练掌握,注意明确有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.


 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:解答题
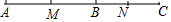 已知M是线段AB的中点,N是线段BC的中点.
已知M是线段AB的中点,N是线段BC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
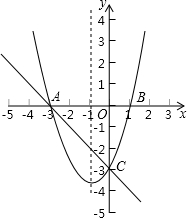 如图:抛物线y1=ax2+bx+c与直线y2=kx+b交于A(-3,0)、C(0,-3)两点,抛物线与x轴交于另一点B(1,0).利用图象填空:
如图:抛物线y1=ax2+bx+c与直线y2=kx+b交于A(-3,0)、C(0,-3)两点,抛物线与x轴交于另一点B(1,0).利用图象填空:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
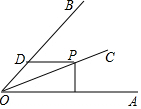 如图,OC平分∠AOB=60°,且∠AOB=60°,点P为OC上任意点,PM⊥OA于M,PD∥OA,交OB于D,若OM=6,则PD的长为( )
如图,OC平分∠AOB=60°,且∠AOB=60°,点P为OC上任意点,PM⊥OA于M,PD∥OA,交OB于D,若OM=6,则PD的长为( )| A. | 3 | B. | 4 | C. | 4.5 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com