练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图,△ABC中,AB=AC,∠BAC=90°,D是BC边上任意一点,求证：BD+CD=2AD.

    【答案】见解析

    【解析】

    作AE⊥BC于E，由于∠BAC=90°，AB=AC，所以BE=CE，要证明BD+CD=2AD，只需找出BD、CD、AD三者之间的关系即可，由勾股定理可得出AD=AE+ED，AE=AB-BE=AC-CE，ED=BD-BE=CE-CD，代入求出三者之间的关系即可得证．

    证明：作AE⊥BC于E，如图所示：

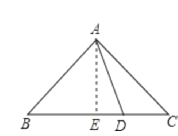
    由题意得：ED=BDBE=CECD，

    ∵在△ABC中,∠BAC=90°，AB=AC，

    ∴BE=CE=BC，

    由勾股定理可得：

    AB+AC=BC，

    AE=ABBE=ACCE，，

    AD=AE+ED，

    2ADimg src="http://thumb.zyjl.cn/questionBank/Upload/2020/11/22/06/793bb150/SYS202011220603314423751839_DA/SYS202011220603314423751839_DA.001.png" width="11" height="20" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />=2AE+2ED=ABBE+(BDBE) +ACCE+(CECD)

    =AB+AC+BD+CD2BD×BE2CD×CE=AB+AC+BD+CD2×BC×BC

    =BD+CD,

    即,BD+CD=2AD

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，D为AB边上一点，E为CD中点，AC=，∠ABC=30°，∠A=∠BED=45°，则BD的长为（　　）

    A. B. +1﹣ C. ﹣ D. ﹣1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

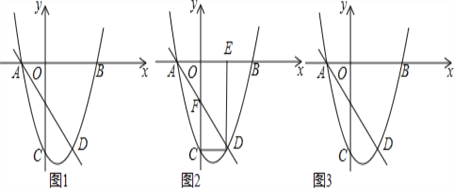
    【题目】如图1，直线AD对应的函数关系式为y=﹣2x﹣2，与抛物线交于点A（在x轴上），点D．抛物线与x轴另一交点为B（3，0），抛物线与y轴交点C（0，﹣6）．

    （1）求抛物线的解析式；

    （2）如图2，连结CD，过点D作x轴的垂线，垂足为点E，直线AD与y轴交点为F，若点P由点D出发以每秒1个单位的速度沿DE边向点E移动，1秒后点Q也由点D出发以每秒3个单位的速度沿DC，CO，OE边向点E移动，当其中一个点到达终点时另一个点也停止移动，点P的移动时间为t秒，当PQ⊥DF时，求t的值；（图3为备用图）

    （3）如果点M是直线BC上的动点，是否存在一个点M，使△ABM中有一个角为45°？如果存在，直接写出所有满足条件的M点坐标；如果不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系 中，函数的图象与直线交于点A(3,m).

    （1）求k、m的值；

    （2）已知点P(n，n)(n>0)，过点P作平行于轴的直线，交直线y=x-2于点M，过点P作平行于y轴的直线，交函数 的图象于点N.

    ①当n=1时，判断线段PM与PN的数量关系，并说明理由；

    ②若PN≥PM，结合函数的图象，直接写出n的取值范围.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

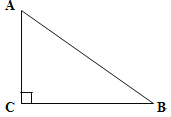
    【题目】如图，已知△ABC，∠C=90，AC<BC，D为BC上一点，且到A，B两点的距离相等.

    （1）用直尺和圆规，作出点D的位置（不写作法，保留作图痕迹）；

    （2）连结AD，若∠B=37°，则∠CAD=_________度.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，点P是直角三角形ABC斜边AB上一动点（不与A，B重合），分别过A，B向直线CP作垂线，垂足分别为E，F，Q为斜边AB的中点．

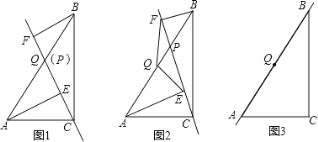
    （1）如图1，当点P与点Q重合时，AE与BF的位置关系是　 　，QE与QF的数量关系式　 　；

    （2）如图2，当点P在线段AB上不与点Q重合时，试判断QE与QF的数量关系，并给予证明；

    （3）如图3，当点P在线段BA（或AB）的延长线上时，此时（2）中的结论是否成立？请画出图形并给予证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

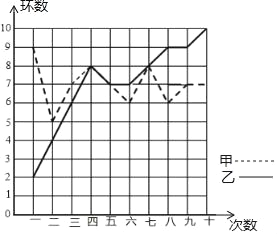
    【题目】某市射击队甲、乙两名队员在相同的条件下各射耙10次，每次射耙的成绩情况如图所示：

    （1）请将下表补充完整：（参考公式：方差S2= [（x1﹣）2+（x2﹣）2+…+（xn﹣）2]）

    平均数

    方差

    中位数

    甲

    7

    　 　

    7

    乙

    　 　

    5.4

    　 　

    （2）请从下列三个不同的角度对这次测试结果进行

    ①从平均数和方差相结合看，　 　的成绩好些；

    ②从平均数和中位数相结合看，　 　的成绩好些；

    ③若其他队选手最好成绩在9环左右，现要选一人参赛，你认为选谁参加，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某种商品的定价为每件20元，商场为了促销，决定如果购买5件以上，则超过5件的部分打7折．

    （1）求购买这种商品的货款y （元）与购买数量x （件）之间的函数关系；

    （2）当x=3，x=6时，货款分别为多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】大家知道，它在数轴上表示5的点与原点(即表示0的点)之间的距离.又如式子,它在数轴上的意义是表示6的点与表示3的点之间的距离.即点A、B在数轴上分别表示数a、b,则A、B两点的距离可表示为:|AB|=.根据

    以上信息，回答下列问题：

    (1)数轴上表示2和5的两点之间的距离是 ；数轴上表示-2和-5的两点之间的距离是 .

    （2）点A、B在数轴上分别表示实数x和.

    ①用代数式表示A、B两点之间的距；

    ②如果,求x的值.

    （3）直接写出代数式的最小值.

    查看答案和解析>>

    同步练习册答案