
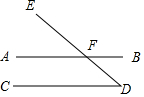
 如图,∠D=49°,∠BFE=131°,试用三种不同的方法说明AB∥CD.
如图,∠D=49°,∠BFE=131°,试用三种不同的方法说明AB∥CD. 分析 根据同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行,分别判定AB∥CD即可.
解答  解:方法一
解:方法一
∵∠BFE=131°,
∴∠AFE=180°-131°=49°,
又∵∠D=49°,
∴∠D=∠AFE,
∴AB∥CD;
方法二
∵∠BFE=131°,
∴∠BFD=180°-131°=49°,
又∵∠D=49°,
∴∠D=∠BFD,
∴AB∥CD;
方法三
∵∠BFE=131°,
∴∠AFD=131°,
又∵∠D=49°,
∴∠D+∠AFD=180°,
∴AB∥CD.
点评 本题考查平行线的判定,熟练掌握平行线的判定方法是解决问题的关键,记住同位角相等两直线平行,内错角相等两直线平行,同旁内角互补两直线平行是关键.


 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:解答题
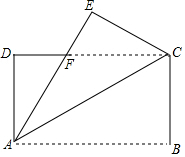 如图,将一个长方形纸片ABCD沿对角线AC折叠,点B落在点E处,AE交DC于点F,已知AB=4cm,BC=2cm,求折叠后重合部分的面积.
如图,将一个长方形纸片ABCD沿对角线AC折叠,点B落在点E处,AE交DC于点F,已知AB=4cm,BC=2cm,求折叠后重合部分的面积.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
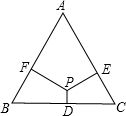 如图,P为等腰△ABC内一点,过点P分别作三条边BC、CA、AB的垂线,垂足分别为D、E、F,已知AB=AC=10,BC=12,且PD:PE:PF=1:3:3,则AP的长为( )
如图,P为等腰△ABC内一点,过点P分别作三条边BC、CA、AB的垂线,垂足分别为D、E、F,已知AB=AC=10,BC=12,且PD:PE:PF=1:3:3,则AP的长为( )| A. | $\frac{4}{3}$ | B. | $\frac{20}{3}$ | C. | 7 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
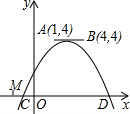 如图,点A,B的坐标分别为(1,4)和(4,4),将抛物线y=a(x-m)2+n平移并保持顶点在线段AB上,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为-3,则当点D的横坐标达到最大值时抛物线的解析式为y=-$\frac{1}{4}$(x-4)2+4.
如图,点A,B的坐标分别为(1,4)和(4,4),将抛物线y=a(x-m)2+n平移并保持顶点在线段AB上,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为-3,则当点D的横坐标达到最大值时抛物线的解析式为y=-$\frac{1}{4}$(x-4)2+4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{18}$ | B. | $\sqrt{\frac{3}{4}}$ | C. | $\sqrt{12}$ | D. | -$\sqrt{27}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
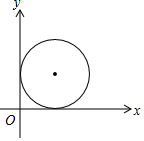 如图,在平面直角坐标系中,放置半径为1的圆,与两坐标轴相切,若该圆向x轴正方向滚动2017圈后(滚动时在x轴上不滑动),则该圆的圆心坐标为( )
如图,在平面直角坐标系中,放置半径为1的圆,与两坐标轴相切,若该圆向x轴正方向滚动2017圈后(滚动时在x轴上不滑动),则该圆的圆心坐标为( )| A. | (2018,1) | B. | (4034π+1,1) | C. | (2017,1) | D. | (4034π-1,1) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知在?ABCD中,点E是边AD上一点,将△ABE沿BE翻折,点A正好落在CD边上的点F处,若△DEF的周长为10cm,△BCF的周长为24cm,则CF的长为( )
如图,已知在?ABCD中,点E是边AD上一点,将△ABE沿BE翻折,点A正好落在CD边上的点F处,若△DEF的周长为10cm,△BCF的周长为24cm,则CF的长为( )| A. | 6cm | B. | 7cm | C. | 10cm | D. | 12cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com