
 如图,已知在?ABCD中,点E是边AD上一点,将△ABE沿BE翻折,点A正好落在CD边上的点F处,若△DEF的周长为10cm,△BCF的周长为24cm,则CF的长为( )
如图,已知在?ABCD中,点E是边AD上一点,将△ABE沿BE翻折,点A正好落在CD边上的点F处,若△DEF的周长为10cm,△BCF的周长为24cm,则CF的长为( )| A. | 6cm | B. | 7cm | C. | 10cm | D. | 12cm |
分析 根据折叠的性质可得EF=AE、BF=BA,从而?ABCD的周长可转化为:△FDE的周长+△FCB的周长,求出AB+BC,再由△FCB的周长为42,求出FC的长,即可解决问题.
解答 解:由折叠的性质可得EF=AE、BF=AB,
∴?ABCD的周长=DF+FC+CB+BA+AE+DE=△FDE的周长+△FCB的周长=10+24=34,
∵四边形ABCD为平行四边形,
∴AB+BC=17,
∵△FCB的周长=CF+BC+BF=CF+BC+AB=24,
即FC+17=24,
∴FC=7cm,
故选B.
点评 本题主要考查了翻折变换的性质、平行四边形的性质等几何知识点;根据折叠的性质将平行四边形的周长与△FCB的周长进行转化是解决问题的关键.


科目:初中数学 来源: 题型:解答题
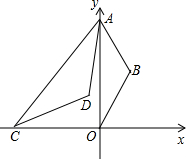 如图,点A为y轴正半轴上一点,以OA为底边向y轴右侧作等腰三角形OAB,使得∠B=120°,C为x轴上一点,连接AC,以AC为底边向右侧作等腰三角形ACD,使得∠D=120°.
如图,点A为y轴正半轴上一点,以OA为底边向y轴右侧作等腰三角形OAB,使得∠B=120°,C为x轴上一点,连接AC,以AC为底边向右侧作等腰三角形ACD,使得∠D=120°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2.1×108 | B. | 21×108 | C. | 2.1×109 | D. | 0.21×1010 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.312×106人 | B. | 1.312×107人 | C. | 13.12×106人 | D. | 0.1312×108人 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{4000}{x}=\frac{4000}{x+10}+20$ | B. | $\frac{4000}{x}=\frac{4000}{x-10}-2}$ | ||
| C. | $\frac{4000}{x+10}=\frac{4000}{x}+20$ | D. | $\frac{4000}{x-10}=\frac{4000}{x}-20$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com