
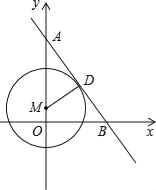
【题目】如图,已知直线y=﹣2x+12分别与y轴,x轴交于A,B两点,点M在y轴上,以点M为圆心的⊙M与直线AB相切于点D,连接MD.
(1)求证:△ADM∽△AOB;
(2)如果⊙M的半径为2![]() ,请写出点M的坐标,并写出以(﹣
,请写出点M的坐标,并写出以(﹣![]() ,
, ![]() )为顶点,且过点M的抛物线的解析式.
)为顶点,且过点M的抛物线的解析式.
【答案】(1)见解析;(2)y=﹣2(x+![]() )2+
)2+![]() .
.
【解析】试题分析:(1)由AB为圆M的切线,利用切线的性质得到一对角为直角,再由公共角,利用两对角相等的三角形相似即可得证;
(2)设M(0,m),表示出AM,求出DM的长,利用勾股定理求出AB的长,由三角形相似得比例,求出m的值,求出M坐标,设出抛物线顶点形式,把M坐标代入求出即可.
试题解析:(1)证明:∵AB是⊙M切线,D是切点,
∴MD⊥AB,
∴∠MDA=∠AOB=90°,
又∠MAD=∠BAO,
∴△ADM∽△AOB;
(2)解:设M(0,m),
由直线y=2x+12得,OA=12,OB=6,
则AM=12﹣m,DM=2![]() ,
,
在Rt△AOB中,AB=![]() =
=![]() =6
=6![]() ,
,
∵△ADM∽△AOB,
∴![]() ,即
,即![]() ,
,
解得:m=2,
∴M(0,2),
设顶点为(﹣![]() ,
, ![]() )的抛物线解析式为y=a(x+
)的抛物线解析式为y=a(x+![]() )2+
)2+![]() ,
,
将M点坐标代入,得a(0+![]() )2+
)2+![]() =2,
=2,
解得:a=﹣2,
则抛物线解析式为y=﹣2(x+![]() )2+
)2+![]() .
.


科目:初中数学 来源: 题型:
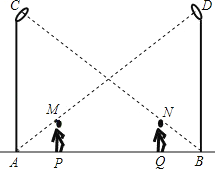
【题目】如图,王华同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行12m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部.已知王华同学的身高是1.6m,两个路灯的高度都是9.6m.
(1)求两个路灯之间的距离;
(2)当王华同学走到路灯BD处时,他在路灯AC下的影子长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
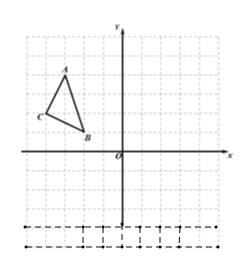
【题目】如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度,△ABC的顶点均在格点上,三个顶点的坐标分别是A(-3,4),B(-2,1),C(-4,2).
(1)将△ABC先向右平移7个单位长度,再向上平移2个单位长度,画出第二次平移后的△![]() ;
;
(2)以点O(0,0)为对称中心,画出与△ABC成中心对称的△![]() ;
;
(3)将点B绕坐标原点逆时针方向旋转90°至点![]() ,则点
,则点![]() 的坐标为(______,______)
的坐标为(______,______)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)把数轴补充完整.
(2)在数轴上表示下列各数.
(3)用“<”连接起来. .
(4)﹣|﹣2|与﹣4之间的距离是 .
3![]() ,﹣4,﹣(﹣1.5),﹣|﹣2|
,﹣4,﹣(﹣1.5),﹣|﹣2|
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为准备母亲节礼物,同学们委托小明用其支付宝余额团购鲜花或礼盒.每束鲜花的售价相同,每份礼盒的售价也相同.若团购15束鲜花和18份礼盒,余额差80元;若团购18束鲜花和15份礼盒,余额剩70元.若团购19束鲜花和14份礼盒,则支付宝余额剩_______元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC的垂直平分线EF交∠ABC的平分线BD于E,如果∠BAC=60°,∠ACE=24°,那么∠BCE的大小是( )

A. 24° B. 30° C. 32° D. 36°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,点A,B,C,D在一条直线上,填写下列空格:
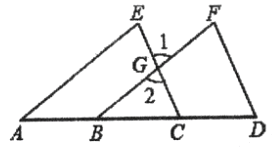
∵AE∥BF(已知)
∴∠E=∠1(______________________)
∵∠E=∠F(已知〉
∴∠_____=∠F(________________)
∴________∥_________(________________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
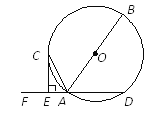
【题目】如图,AB是⊙O的直径,AD是⊙O的弦,点F是DA延长线上的一点,过⊙O上一点C作⊙O的切线交DF于点E,CE⊥DF.
(1)求证:AC平分∠FAB;
(2)若AE=1,CE=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
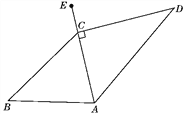
【题目】为倡导“低碳生活”,人们常选择以自行车作为代步工具,如图是一辆自行车的部分几何示意图,其中车架档AC与CD的长分别为45 cm和60 cm,且它们互相垂直,座杆CE的长为20 cm,点A,C,E在同一条直线上,且∠CAB=75°.(参考数据:sin 75°≈0.966,cos 75°≈0.259,tan 75°≈3.732)
(1)求车架档AD的长;
(2)求车座点E到车架档AB的距离(结果精确到1 cm).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com