
【题目】已知,在正方形ABCD中,E是CB延长线上一点,且EB=![]() BC,F是AB的中点,请你将F点与图中某一标明字母的点连接成线段,使连成的线段与AE相等.并证明这种相等关系.
BC,F是AB的中点,请你将F点与图中某一标明字母的点连接成线段,使连成的线段与AE相等.并证明这种相等关系.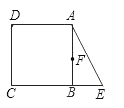
【答案】解:如图,连接DF、CF均可得出与AE相等.
证明:∵ABCD为正方形,
∴AD=AB,∠DAF=∠ABE,
∵F为中点,BE=![]() BC,
BC,
∴AF=BE,
∴△ADF≌△BAF,
∴DF=AE.
同理可得CF=AE.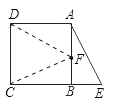
【解析】根据题意可以知道连接CF、DF均可,可以根据三角形全等证明.
【考点精析】本题主要考查了正方形的性质的相关知识点,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题.


科目:初中数学 来源: 题型:
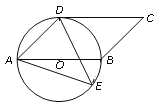
【题目】如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45.
(1)试判断CD与⊙O的位置关系,并证明你的结论;
(2)若⊙O的半径为3,sin∠ADE=![]() ,求AE的值.
,求AE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
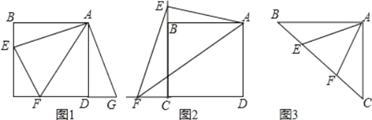
【题目】【发现证明】
如图1,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,试判断BE,EF,FD之间的数量关系.
小聪把△ABE绕点A逆时针旋转90°至△ADG,通过证明△AEF≌△AGF;从而发现并证明了EF=BE+FD.
【类比引申】
(1)如图2,点E、F分别在正方形ABCD的边CB、CD的延长线上,∠EAF=45°,连接EF,请根据小聪的发现给你的启示写出EF、BE、DF之间的数量关系,并证明;
【联想拓展】
(2)如图3,如图,∠BAC=90°,AB=AC,点E、F在边BC上,且∠EAF=45°,若BE=3,EF=5,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小林在某店购买A、B商品共三次,只有一次购买时,商品A、B同时打折,其余两次均按标价购买,三次购买商品A、B的数量和费用如下表:
购买商品A的数量(个) | 购买商品B的数量(个) | 购买总费用(元) | |
第一次购物 | 6 | 5 | 1140 |
第二次购物 | 3 | 7 | 1110 |
第三次购物 | 9 | 8 | 1062 |
(1)小林以折扣价购买商品A、B是第次购物;
(2)求出商品A、B的标价;
(3)若商品A、B的折扣相同,问商店是打几折出售这两种商品的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为丰富学生课外活动,某校积极开展社团活动,学生可根据自己的爱好选择一项,已知该校开设的体育社团有:A:篮球,B:排球C:足球;D:羽毛球,E:乒乓球.李老师对某年级同学选择体育社团情况进行调查统计,制成了两幅不完整的统计图(如图),则以下结论不正确的是( )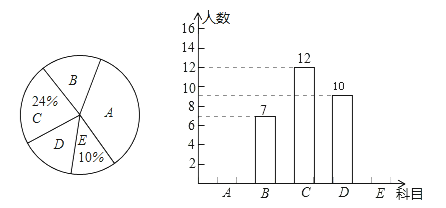
A.选科目E的有5人
B.选科目D的扇形圆心角是72°
C.选科目A的人数占体育社团人数的一半
D.选科目B的扇形圆心角比选科目D的扇形圆心角的度数少21.6°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com