
【题目】如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45.
(1)试判断CD与⊙O的位置关系,并证明你的结论;
(2)若⊙O的半径为3,sin∠ADE=![]() ,求AE的值.
,求AE的值.
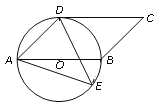
【答案】(1)CD与圆O相切,证明见解析;(2)AE=5 .
【解析】(1)连接OD,则∠AOD=为直角,由四边形ABCD是平行四边形,则AB∥CD,从而得出∠CDO=90°,即可证出答案.
(2)连接BE,则∠ADE=∠ABE,根据题意得sin∠ABE=![]() . 由AB是圆O的直径求出AB的长.再在Rt△ABE中,求得AE即可.
. 由AB是圆O的直径求出AB的长.再在Rt△ABE中,求得AE即可.
解:(1)CD与圆O相切. 证明:连接OD,则∠AOD=2∠AED =2×450=900.
∵四边形ABCD是平行四边形,∴AB//DC.∴∠CDO=∠AOD=90°.∴OD⊥CD. ∴CD与圆O相切
(2)连接BE,则∠ADE=∠ABE. ∴sin∠ADE=sin∠ABE=![]() .
.
∵AB是圆O的直径,∴∠AEB=900,AB=2×3=6.
在Rt△ABE中,sin∠ABE=![]() .∴AE=5 .
.∴AE=5 .
“点睛”此题考查了切线的判定、圆周角定理、垂线定理、平行四边形的性质以及三角函数等知识.此题综合性较强,难度适中,注意掌握辅助线的作法,注意数形结合思想与转化思想的应用.


科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,CD与⊙O相切于点C,DA⊥AB,DO及DO的延长线与⊙O分别相交于点E、F,EB与CF相交于点G.
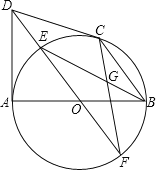
(1)求证:DA=DC;
(2)⊙O的半径为3,DC=4,求CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验初中组织了“英语手抄报”征集活动,现从中随机抽取部分作品,按A、B、C、D四个等级进行评价,并根据统计结果绘制了如下两幅不完整的统计图.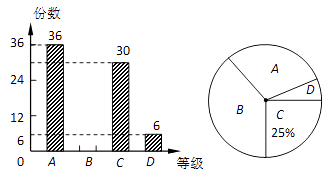
(1)抽取了份作品;
(2)此次抽取的作品中等级为B的作品有份,并补全条形统计图;
(3)若该校共征集到600份作品,请估计等级为A的作品约有多少份?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在正方形ABCD中,E是CB延长线上一点,且EB=![]() BC,F是AB的中点,请你将F点与图中某一标明字母的点连接成线段,使连成的线段与AE相等.并证明这种相等关系.
BC,F是AB的中点,请你将F点与图中某一标明字母的点连接成线段,使连成的线段与AE相等.并证明这种相等关系.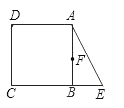
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com