
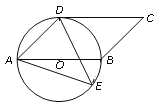
【题目】如图,AB是⊙O的直径,CD与⊙O相切于点C,DA⊥AB,DO及DO的延长线与⊙O分别相交于点E、F,EB与CF相交于点G.
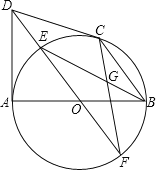
(1)求证:DA=DC;
(2)⊙O的半径为3,DC=4,求CG的长.
【答案】解:(1)证明:连接OC,
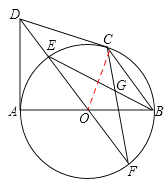
∵DC是⊙O切线,∴OC⊥DC。
∵OA⊥DA,∴∠DAO=∠DCO=90°。
在Rt△DAO和Rt△DCO中,
∵DO=DO,OA=OC,
∴Rt△DAO≌Rt△DCO(HL)。
∴DA=DC.
(2)连接BF、CE、AC,设AC与OD相交于点M,
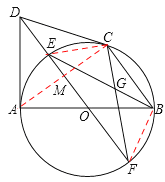
由切线长定理得:DC=DA=4,DO⊥AC,
∴DO平分AC。
在Rt△DAO中,AO=3,AD=4,
由勾股定理得:DO=5。
∵由三角形面积公式得:![]() DAAO=
DAAO=![]() DOAM,
DOAM,
则AM=![]() 。
。
同理CM=AM=![]() 。∴AC=
。∴AC=![]() 。
。
∵AB是直径,∴∠ACB=90°。
由勾股定理得:![]() 。
。
∵由圆周角定理得∠GCB=∠GEF,∠GFE=∠GBC,∴△BGC∽△EGF。
∴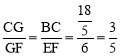 。
。
在Rt△OMC中,CM=![]() ,OC=3,由勾股定理得:OM=
,OC=3,由勾股定理得:OM=![]() 。
。
在Rt△EMC中,CM=![]() ,ME=OE﹣OM=3﹣
,ME=OE﹣OM=3﹣![]() =
=![]() ,由勾股定理得:CE=
,由勾股定理得:CE=![]() 。
。
在Rt△CEF中,EF=6,CE=![]() ,由勾股定理得:CF=
,由勾股定理得:CF=![]() 。
。
∵CF=CG+GF,![]() ,∴CG=
,∴CG=![]() CF=
CF=![]() ×
×![]() =
=![]() 。
。
【解析】
试题分析:(1)连接OC,∠DAO=∠DCO=90°,根据HL证Rt△DAO≌Rt△DCO,根据全等三角形的性质推出即可。
(2)连接BF、CE、AC,由切线长定理求出DC=DA=4,求出DO=5,CM、AM的长,由勾股定理求出BC长,根据△BGC∽△EGF求出![]() ,则CG=
,则CG=![]() CF;利用勾股定理求出CF的长,则CG的长度可求得。
CF;利用勾股定理求出CF的长,则CG的长度可求得。


科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=2,AD=3,点E是BC边上靠近点B的三等分点,动点P从点A出发,沿路径A→D→C→E运动,则△APE的面积y与点P经过的路径长x之间的函数关系用图象表示大致是( )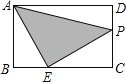
A.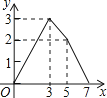
B.
C.
D.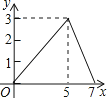
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作:某数学兴趣小组在研究用一副三角板拼角时,小明、小亮分别拼出图1、图2所示的两种图形,如图1,小明把30°和90°的角按如图1方式拼在一起;小亮把30°和90°的角按如图2方式拼在一起,并在各自所拼的图形中分别作出∠AOB、∠COD的平分线OE、OF.小明很容易地计算出图1中∠EOF=60°.
计算:请你计算出图2中∠EOF=度.
归纳:通过上面的计算猜一猜,当有公共顶点的两个角∠α、∠β有一条边重合,且这两个角在公共边的异侧时,则这两个角的平分线所夹的角= . (用含α、β的代数式表示)
拓展:小明把图1中的三角板AOB绕点O顺时针旋转90°后得到图3,小亮把图2中的三角板AOB绕点O顺时针旋转90°后得到图4(两图中的点O、B、D在同一条直线上).在图3中,易得到∠EOF=∠DOF﹣∠BOE= ![]() ∠COD﹣
∠COD﹣ ![]() ∠AOB=45°﹣15°=30°;仿照图3的作法,请你通过计算,求出图4中∠EOF的度数(写出解答过程).
∠AOB=45°﹣15°=30°;仿照图3的作法,请你通过计算,求出图4中∠EOF的度数(写出解答过程).
反思:通过上面的拓展猜一猜,当有公共顶点的两个角∠α、∠β(∠α>∠β)有一条边重合,且这两个角在公共边的同侧时,则这两个角的平分线所夹的角= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校计划用地面砖铺设教学楼前矩形广场的地面ABCD已知矩形广场地面的长为100米,宽为80米.图案设计如图所示:广场的四角为小正方形,阴影部分为四个矩形,四个矩形的宽都为小正方形的边长,阴影部分铺绿色地面砖,其余部分铺白色地面砖.
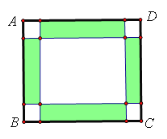
(1)要使铺白色地面砖的面积为5200平方米,则矩形广场四角的小正方形的边长为多少米?
(2)如果铺白色地面砖的费用为每平方米30元,铺绿色地面砖的费用为每平方米20元.当广场四角小正方形的边长为多少米时,铺广场地面的总费用最少?最少费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45.
(1)试判断CD与⊙O的位置关系,并证明你的结论;
(2)若⊙O的半径为3,sin∠ADE=![]() ,求AE的值.
,求AE的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com