
【题目】操作:某数学兴趣小组在研究用一副三角板拼角时,小明、小亮分别拼出图1、图2所示的两种图形,如图1,小明把30°和90°的角按如图1方式拼在一起;小亮把30°和90°的角按如图2方式拼在一起,并在各自所拼的图形中分别作出∠AOB、∠COD的平分线OE、OF.小明很容易地计算出图1中∠EOF=60°.
计算:请你计算出图2中∠EOF=度.
归纳:通过上面的计算猜一猜,当有公共顶点的两个角∠α、∠β有一条边重合,且这两个角在公共边的异侧时,则这两个角的平分线所夹的角= . (用含α、β的代数式表示)
拓展:小明把图1中的三角板AOB绕点O顺时针旋转90°后得到图3,小亮把图2中的三角板AOB绕点O顺时针旋转90°后得到图4(两图中的点O、B、D在同一条直线上).在图3中,易得到∠EOF=∠DOF﹣∠BOE= ![]() ∠COD﹣
∠COD﹣ ![]() ∠AOB=45°﹣15°=30°;仿照图3的作法,请你通过计算,求出图4中∠EOF的度数(写出解答过程).
∠AOB=45°﹣15°=30°;仿照图3的作法,请你通过计算,求出图4中∠EOF的度数(写出解答过程).
反思:通过上面的拓展猜一猜,当有公共顶点的两个角∠α、∠β(∠α>∠β)有一条边重合,且这两个角在公共边的同侧时,则这两个角的平分线所夹的角= .
科目:初中数学 来源: 题型:
【题目】将点P(m+2,2m+4)向右平移1个单位长度得到点M,且点M在y轴上,那么点M的坐标是( )
A. (-2,0) B. (0,-2) C. (1,0) D. (0,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,抛物线![]() 经过点A(0,-3),B(4,5).
经过点A(0,-3),B(4,5).
(1)求此抛物线表达式及顶点M的坐标;
(2)设点M关于y轴的对称点是N,此抛物线在A,B两点之间的部分记为图象W(包含A,B两点),经过点N的直线l: ![]() 与图象W恰一个有公共点,结合图象,求m的取值范围.
与图象W恰一个有公共点,结合图象,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解南山荔枝的销售情况,某部门对该市场的三种荔枝品种A、B、C在6月上半月的销售进行调查统计,绘制成如下两个统计图(均不完整).请你结合图中的信息,解答下列问题:
(1)该市场6月上半月共销售这三种荔枝多少吨?
(2)补全图1的统计图并计算图2中A所在扇形的圆心角的度数.
(3)某商场计划六月下半月进货A、B、C三种荔枝共300千克,根据该市场6月上半月的销售情况,求该商场应购进C品种荔枝多少千克比较合理?
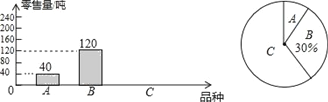
(图1) (图2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】陈杰骑自行车去上学,当他以往常的速度骑了一段路时,忽然想起要买某本书,于是又折回到刚经过的一家书店,买到书后继续赶去学校.以下是他本次上学所用的路程与时间的关系示意图.根据图中提供的信息回答下列问题: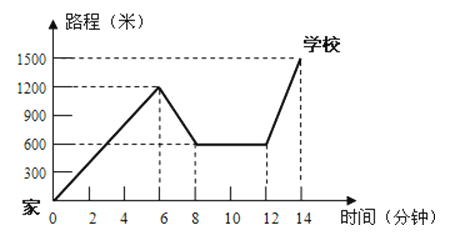
(1)陈杰家到学校的距离是多少米?书店到学校的距离是多少米?
(2)陈杰在书店停留了多少分钟?本次上学途中,陈杰一共行驶了多少米?
(3)在整个上学的途中哪个时间段陈杰骑车速度最快?最快的速度是多少米?
(4)如果陈杰不买书,以往常的速度去学校,需要多少分钟?本次上学比往常多用多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,CD与⊙O相切于点C,DA⊥AB,DO及DO的延长线与⊙O分别相交于点E、F,EB与CF相交于点G.
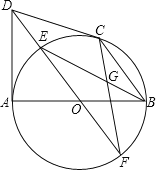
(1)求证:DA=DC;
(2)⊙O的半径为3,DC=4,求CG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com