
 x2+mx+n(n≠0)与直线y=x交于A、B两点,与y轴交于点C,OA=OB,BC∥x轴.
x2+mx+n(n≠0)与直线y=x交于A、B两点,与y轴交于点C,OA=OB,BC∥x轴. ,过D、E两点分别作y轴的平行线,交抛物线于F、G,若设D点的横坐标为x,四边形DEGF的面积为y,求x与y之间的关系式,写出自变量x的取值范围,并回答x为何值时,y有最大值.
,过D、E两点分别作y轴的平行线,交抛物线于F、G,若设D点的横坐标为x,四边形DEGF的面积为y,求x与y之间的关系式,写出自变量x的取值范围,并回答x为何值时,y有最大值.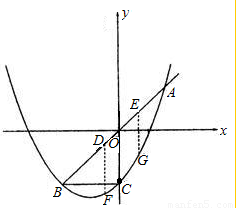
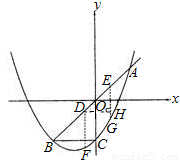 解:(1)∵抛物线y=
解:(1)∵抛物线y= x2+mx+n与y轴交于点C
x2+mx+n与y轴交于点C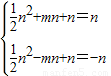
 x2+x-2
x2+x-2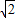
 x2+x-2,
x2+x-2, (x+1)2+(x+1)-2
(x+1)2+(x+1)-2 x2+x-2)=2-
x2+x-2)=2- x2,EG=(x+1)-[
x2,EG=(x+1)-[ (x+1)2+(x+1)-2]=2-
(x+1)2+(x+1)-2]=2- (x+1)2
(x+1)2 [2-
[2- x2+2-
x2+2- (x+1)2]×1
(x+1)2]×1 x2-
x2- x+
x+ ,
, (x+
(x+ )2+
)2+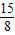 ,
, 时,y最大值=
时,y最大值=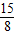 .
.

科目:初中数学 来源:2010年中考数学考前10日信息题复习题精选(5)(解析版) 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2010年湖北省黄冈市数学中考精品试卷之三(解析版) 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2009年云南省楚雄州双柏县中考数学模拟试卷(大庄中学 谭金平)(解析版) 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2009年江苏省盐城市初级中学中考数学模拟试卷(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com