
【题目】如图,在平面直角坐标系中,一次函数y=kx+b与反比例函数y=![]() (m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(1)求反比例函数和一次函数的表达式;
(2)如果点P是x轴上一点,且△ABP的面积是3,求点P的坐标.

【答案】(1)y=![]() ;y=x-2;(2)(0,0)或(4,0)
;y=x-2;(2)(0,0)或(4,0)
【解析】试题分析:(1)利用待定系数法即可求得函数的解析式;
(2)首先求得AB与x轴的交点,设交点是C,然后根据S△ABP=S△ACP+S△BCP即可列方程求得P的横坐标.
试题解析:(1)∵反比例函数y=![]() (m≠0)的图象过点A(3,1),
(m≠0)的图象过点A(3,1),
∴3=![]()
∴m=3.
∴反比例函数的表达式为y=![]() .
.
∵一次函数y=kx+b的图象过点A(3,1)和B(0,-2).
∴![]() ,
,
解得: ![]() ,
,
∴一次函数的表达式为y=x-2;
(2)令y=0,∴x-2=0,x=2,
∴一次函数y=x-2的图象与x轴的交点C的坐标为(2,0).
∵S△ABP=3,
![]() PC×1+
PC×1+![]() PC×2=3.
PC×2=3.
∴PC=2,
∴点P的坐标为(0,0)、(4,0).


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
【题目】某公司招聘人才,对应聘者分别进行阅读能力、思维能力和表达能力三项测试,其中甲、乙两人的成绩如表(单位:分):
项目人员 | 阅读能力 | 思维能力 | 表达能力 |
甲 | 93 | 86 | 73 |
乙 | 95 | 81 | 79 |
(1)若根据三项测试的平均成绩在甲、乙两人中录用一人,那么谁将能被录用?
(2)根据实际需要,公司将阅读、思维和表达能力三项测试得分按3:5:2的比确定每人的最后成绩,若按此成绩在甲、乙两人中录用一人,谁将被录用?
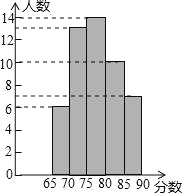
(3)公司按照(2)中的成绩计算方法,将每位应聘者的最后成绩绘制成如图所示的频数分布直方图(每组分数段均包含左端数值,不包含右端数值,如最右边一组分数x为:85≤x<90),并决定由高分到低分录用8名员工,甲、乙两人能否被录用?请说明理由,并求出本次招聘人才的录用率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜经销商去蔬菜生产基地批发某种蔬菜,已知这种蔬菜的批发量在20千克~60千克之间(含20千克和60千克)时,每千克批发价是5元;若超过60千克时,批发的这种蔬菜全部打八折,但批发总金额不得少于300元.
(1)根据题意,填写如表:
蔬菜的批发量(千克) | … | 25 | 60 | 75 | 90 | … |
所付的金额(元) | … | 125 | 300 | … |
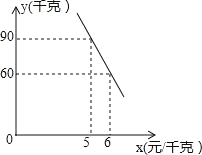
(2)经调查,该蔬菜经销商销售该种蔬菜的日销售量y(千克)与零售价x(元/千克)是一次函数关系,其图象如图,求出y与x之间的函数关系式;
(3)若该蔬菜经销商每日销售此种蔬菜不低于75千克,且当日零售价不变,那么零售价定为多少时,该经销商销售此种蔬菜的当日利润最大?最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中正确的是( )
A. 两条对角线互相平分的四边形是平行四边形
B. 两条对角线相等的四边形是矩形
C. 两条对角线互相垂直的四边形是菱形
D. 两条对角线互相垂直且平分的四边形是正方形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com