
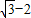 ,∠C=30°,BC边上的高为2.试求:
,∠C=30°,BC边上的高为2.试求:
 ×BC×AD=
×BC×AD= ×(AB+BC+AC)r,求出即可.
×(AB+BC+AC)r,求出即可.
 =2
=2 ,
,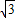 -(2
-(2 -2)=2=AD,
-2)=2=AD, =2
=2 ;
;
 ×BC×AD=
×BC×AD= ×(AB+BC+AC)r,
×(AB+BC+AC)r,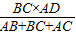 =
= ≈0.35,
≈0.35,

科目:初中数学 来源: 题型:
 (2013•金山区一模)如图,已知一钝角△ABC中,BC=2
(2013•金山区一模)如图,已知一钝角△ABC中,BC=2| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:

| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
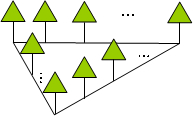 某中学旁边有一块三角形空地,为了保持水土,美化环境,全校师生一齐动手,在空地的三条边上栽上了树苗(如图).已知三边上的树苗数分别为50、14、48,空地的三个角均有一棵树,且每条边上的树苗株距均为1米,那么这块空地的形状为( )
某中学旁边有一块三角形空地,为了保持水土,美化环境,全校师生一齐动手,在空地的三条边上栽上了树苗(如图).已知三边上的树苗数分别为50、14、48,空地的三个角均有一棵树,且每条边上的树苗株距均为1米,那么这块空地的形状为( )查看答案和解析>>
科目:初中数学 来源: 题型:解答题
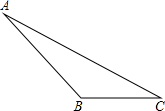 如图,已知一钝角△ABC中,BC=2
如图,已知一钝角△ABC中,BC=2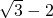 ,∠C=30°,BC边上的高为2.试求:
,∠C=30°,BC边上的高为2.试求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com