
【题目】如图,△ABC边AB上点D、E(不与点A、B重合),满足∠DCE=∠ABC,∠ACB=90°,AC=3,BC=4; 
(1)当CD⊥AB时,求线段BE的长;
(2)当△CDE是等腰三角形时,求线段AD的长;
(3)设AD=x,BE=y,求y关于x的函数解析式,并写出定义域.
【答案】
(1)解:在△ABC中,∠ACB=90°,AC=3,BC=4,
∴AB=5,sinA= ![]() ,tanB=
,tanB= ![]() ,
,
如图,当CD⊥AB时,△ACD为直角三角形,
∴CD=ACsinA= ![]() ,
,
∴AD= ![]() =
= ![]() ,
,
又∵∠DCE=∠ABC,
∴在Rt△CDE中,DE=CDtan∠DCE= ![]() ×
× ![]() =
= ![]() ,
,
∴BE=AB﹣AD﹣DE=5﹣ ![]() ﹣
﹣ ![]() =
= ![]()
(2)解:当△CDE时等腰三角形时,可知∠CDE>∠A>∠B=∠DCE,∠CED>∠B=∠DCE,
∴唯有∠CED=∠CDE,
又∵∠B=∠DCE,∠CDE=∠BDC,
∴∠BCD=∠CED=∠CDE=∠BDC,
∴BD=BC=4,
∴AD=5﹣4=1
(3)解:如图所示,作CH⊥AB于H,
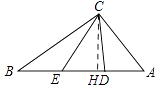
∵ ![]() ×BC×AC=
×BC×AC= ![]() AB×CH,
AB×CH,
∴CH= ![]() ,
,
∴Rt△ACH中,AH= ![]() =
= ![]() ,
,
∴在Rt△CDH中,CD2=CH2+DH2=( ![]() )2+(
)2+( ![]() ﹣x)2=x2﹣
﹣x)2=x2﹣ ![]() x+9,
x+9,
又∵∠CDE=∠BDC,∠DCE=∠B,
∴△BDC∽△CDE,
∴CD2=DEDB,
即x2﹣ ![]() x+9=(5﹣x﹣y)(5﹣x),
x+9=(5﹣x﹣y)(5﹣x),
解得 ![]() .
.
【解析】(1)先根据∠ACB=90°,AC=3,BC=4,求得AB=5,sinA= ![]() ,tanB=
,tanB= ![]() ,再根据△ACD为直角三角形,求得AD,在Rt△CDE中,求得DE,最后根据BE=AB﹣AD﹣DE进行计算即可;(2)当△CDE时等腰三角形时,可知∠CDE>∠A>∠B=∠DCE,∠CED>∠B=∠DCE,进而得出∠CED=∠CDE,再根据∠B=∠DCE,∠CDE=∠BDC,得到∠BCD=∠CED=∠CDE=∠BDC,最后求得AD的长;(3)先作CH⊥AB于H,Rt△ACH中,求得CH和AH的长,在Rt△CDH中,根据勾股定理得出:CD2=x2﹣
,再根据△ACD为直角三角形,求得AD,在Rt△CDE中,求得DE,最后根据BE=AB﹣AD﹣DE进行计算即可;(2)当△CDE时等腰三角形时,可知∠CDE>∠A>∠B=∠DCE,∠CED>∠B=∠DCE,进而得出∠CED=∠CDE,再根据∠B=∠DCE,∠CDE=∠BDC,得到∠BCD=∠CED=∠CDE=∠BDC,最后求得AD的长;(3)先作CH⊥AB于H,Rt△ACH中,求得CH和AH的长,在Rt△CDH中,根据勾股定理得出:CD2=x2﹣ ![]() x+9,再判定△BDC∽△CDE,得出CD2=DEDB,即x2﹣
x+9,再判定△BDC∽△CDE,得出CD2=DEDB,即x2﹣ ![]() x+9=(5﹣x﹣y)(5﹣x),最后求得y关于x的函数解析式,并写出定义域.
x+9=(5﹣x﹣y)(5﹣x),最后求得y关于x的函数解析式,并写出定义域.
【考点精析】认真审题,首先需要了解等腰三角形的性质(等腰三角形的两个底角相等(简称:等边对等角)),还要掌握勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2)的相关知识才是答题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,汽车在东西向的公路l上行驶,途中A,B,C,D四个十字路口都有红绿灯.AB之间的距离为800米,BC为1000米,CD为1400米,且l上各路口的红绿灯设置为:同时亮红灯或同时亮绿灯,每次红(绿)灯亮的时间相同,红灯亮的时间与绿灯亮的时间也相同.若绿灯刚亮时,甲汽车从A路口以每小时30千米的速度沿l向东行驶,同时乙汽车从D路口以相同的速度沿l向西行驶,这两辆汽车通过四个路口时都没有遇到红灯,则每次绿灯亮的时间可能设置为( ) 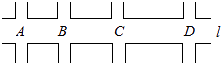
A.50秒
B.45秒
C.40秒
D.35秒
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=3,BC=2,点D是边AB上的动点,过点D作DE∥BC,交边AC于点E,点Q是线段DE上的点,且QE=2DQ,连接BQ并延长,交边AC于点P.设BD=x,AP=y. 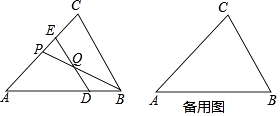
(1)求y关于x的函数解析式及定义域;
(2)当△PQE是等腰三角形时,求BD的长;
(3)连接CQ,当∠CQB和∠CBD互补时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知顶点为A(2,﹣1)的抛物线经过点B(0,3),与x轴交于C、D两点(点C在点D的左侧); 
(1)求这条抛物线的表达式;
(2)联结AB、BD、DA,求△ABD的面积;
(3)点P在x轴正半轴上,如果∠APB=45°,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,AD=3,BC=2,点E、F分别在两腰上, 且EF∥AD,AE:EB=2:1;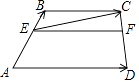
(1)求线段EF的长;
(2)设 ![]() =
= ![]() ,
, ![]() =
= ![]() ,试用
,试用 ![]() 、
、 ![]() 表示向量
表示向量 ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,∠A=30°,BC=6. 
(1)实践操作:尺规作图,不写作法,保留作图痕迹. ①作∠ABC的角平分线交AC于点D.
②作线段BD的垂直平分线,交AB于点E,交BC于点F,连接DE、DF.
(2)推理计算:四边形BFDE的面积为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图1是由5个完全相同的正方体堆成的几何体,现将标有E的正方体平移至如图2所示的位置,下列说法中正确的是( ) 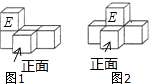
A.左、右两个几何体的主视图相同
B.左、右两个几何体的左视图相同
C.左、右两个几何体的俯视图不相同
D.左、右两个几何体的三视图不相同
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,AB=AC,tan∠B=2,BC=4,D为BC边的中点,点E在BC边的延长线上,且CE=BC,连接AE,F为线段AE的中点 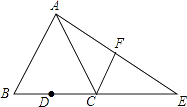
(1)求线段CF的长;
(2)求∠CAE的正弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学课本上,同学们已经探究过“经过已知直线外一点作这条直线的垂线“的尺规作图过程:
已知:直线l和l外一点P
求作:直线l的垂线,使它经过点P.
作法:如图:⑴在直线l上任取两点A、B;
⑵分别以点A、B为圆心,AP,BP长为半径画弧,两弧相交于点Q;
⑶作直线PQ.
参考以上材料作图的方法,解决以下问题:
(1)以上材料作图的依据是:
(2)已知,直线l和l外一点P,
求作:⊙P,使它与直线l相切.(尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com