
【题目】如图,已知在△ABC中,AB=AC,tan∠B=2,BC=4,D为BC边的中点,点E在BC边的延长线上,且CE=BC,连接AE,F为线段AE的中点 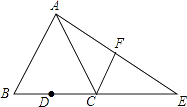
(1)求线段CF的长;
(2)求∠CAE的正弦值.
【答案】
(1)解:如图,连接AD,
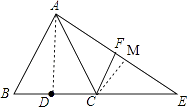
∵AB=AC,且D为BC中点,BC=4,
∴AD⊥BC,BD=CD=2,
∵tanB= ![]() =2,
=2,
∴AD=BDtanB=4,
∴AB=AC= ![]() =
= ![]() =2
=2 ![]() ,
,
又∵BC=CE,AF=EF,
∴CF= ![]() AB=
AB= ![]()
(2)解:如图,过点C作CM⊥AE于点M,
∴∠AMC=∠EMC=90°,
在Rt△ADE中,由勾股定理可得:AE= ![]() =
= ![]() =2
=2 ![]() ,
,
∵由勾股定理得;CM2=AC2﹣AM2=CE2﹣EM2,
∴(2 ![]() )2﹣AM2=42﹣(2
)2﹣AM2=42﹣(2 ![]() ﹣AM)2,
﹣AM)2,
解得:AM= ![]() ,
,
CM= ![]() =
= ![]() =
= ![]() ,
,
∴∠CAE的正弦值是 ![]() =
= ![]() =
= ![]()
【解析】(1)连接AD,由等腰三角形三线合一性质可得AD⊥BC,BD=CD=2,根据tanB= ![]() =2可得AD=4,由勾股定理得AB=AC=2
=2可得AD=4,由勾股定理得AB=AC=2 ![]() ,根据BC=CE、AF=EF即可得CF=
,根据BC=CE、AF=EF即可得CF= ![]() AB.(2)过C作CM⊥AE于M,则∠CMA=∠CME=90°,在Rt△ADE中,由勾股定理求出AE,由勾股定理得出方程(2
AB.(2)过C作CM⊥AE于M,则∠CMA=∠CME=90°,在Rt△ADE中,由勾股定理求出AE,由勾股定理得出方程(2 ![]() )2﹣AM2=42﹣(2
)2﹣AM2=42﹣(2 ![]() ﹣AM)2 , 求出AM,求出CM,即可求出答案.
﹣AM)2 , 求出AM,求出CM,即可求出答案.
【考点精析】认真审题,首先需要了解等腰三角形的性质(等腰三角形的两个底角相等(简称:等边对等角)),还要掌握解直角三角形(解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法))的相关知识才是答题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】课本的作业题中有这样一道题:把一张顶角为36°的等腰三角形纸片剪两刀,分成3张小纸片,使每张小纸片都是等腰三角形,你能办到吗?请画示意图说明剪法. 我们有多少种剪法,图1是其中的一种方法: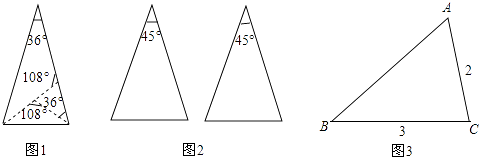
定义:如果两条线段将一个三角形分成3个等腰三角形,我们把这两条线段叫做这个三角形的三分线.
(1)请你在图2中用两种不同的方法画出顶角为45°的等腰三角形的三分线,并标注每个等腰三角形顶角的度数;(若两种方法分得的三角形成3对全等三角形,则视为同一种)
(2)△ABC中,∠B=30°,AD和DE是△ABC的三分线,点D在BC边上,点E在AC边上,且AD=BD,DE=CE,设∠C=x°,试画出示意图,并求出x所有可能的值;
(3)如图3,△ABC中,AC=2,BC=3,∠C=2∠B,请画出△ABC的三分线,并求出三分线的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC边AB上点D、E(不与点A、B重合),满足∠DCE=∠ABC,∠ACB=90°,AC=3,BC=4; 
(1)当CD⊥AB时,求线段BE的长;
(2)当△CDE是等腰三角形时,求线段AD的长;
(3)设AD=x,BE=y,求y关于x的函数解析式,并写出定义域.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4月的某天小欣在“A超市”买了“雀巢巧克力”和“趣多多小饼干”共10包,已知“雀巢巧克力”每包22元,“趣多多小饼干”每包2元,总共花费了80元.
(1)请求出小欣在这次采购中,“雀巢巧克力”和“趣多多小饼干”各买了多少包?
(2)“五一”期间,小欣发现,A、B两超市以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在A超市累计购物超过50元后,超过50元的部分打九折;在B超市累计购物超过100元后,超过100元的部分打八折. ①请问“五一”期间,若小欣购物金额超过100元,去哪家超市购物更划算?
②“五一”期间,小欣又到“B超市”购买了一些“雀巢巧克力”,请问她至少购买多少包时,平均每包价格不超过20元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小学三年级到六年级的全体学生参加“礼仪”知识测试,试题共有10题,每题10分.从中随机抽取了部分学生的成绩进行统计,发现抽测的学生每人至少答对了6题,现将有关数据整理后绘制成如下“年级人数统计图”和尚未全部完成的“成绩情况统计表”.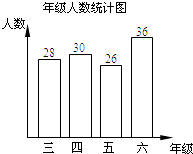
成绩情况统计表
成绩 | 100分 | 90分 | 80分 | 70分 | 60分 |
人数 | 21 | 40 | 5 | ||
频率 | 0.3 |
根据图表中提供的信息,回答下列问题:
(1)请将统计表补充完整
成绩情况统计表
成绩 | 100分 | 90分 | 80分 | 70分 | 60分 |
人数 | 21 | 40 | 5 | ||
频率 | 0.3 |
(2)测试学生中,成绩为80分的学生人数有 名;众数是 分;中位数是 分;
(3)若该小学三年级到六年级共有1800名学生,则可估计出成绩为70分的学生人数约有 名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为4的正方形ABCD内接于点O,点E是 ![]() 上的一动点(不与A、B重合),点F是
上的一动点(不与A、B重合),点F是 ![]() 上的一点,连接OE、OF,分别与AB、BC交于点G,H,且∠EOF=90°,有以下结论,其中正确的个数是( ). ①
上的一点,连接OE、OF,分别与AB、BC交于点G,H,且∠EOF=90°,有以下结论,其中正确的个数是( ). ① ![]() =
= ![]() ; ②△OGH是等腰三角形; ③四边形OGBH的面积随着点E位置的变化而变化;④△GBH周长的最小值为4+
; ②△OGH是等腰三角形; ③四边形OGBH的面积随着点E位置的变化而变化;④△GBH周长的最小值为4+ ![]() .
.
A.1
B.2
C.3
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com