
����Ŀ���α�����ҵ����������һ���⣺��һ�Ŷ���Ϊ36��ĵ���������ֽƬ���������ֳ�3��СֽƬ��ʹÿ��СֽƬ���ǵ��������Σ����ܰ쵽���뻭ʾ��ͼ˵�������� �����ж����ּ�����ͼ1�����е�һ�ַ�����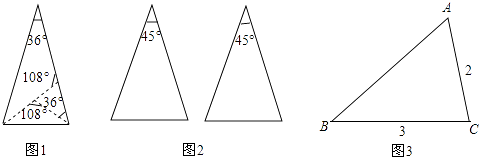
���壺��������߶ν�һ�������ηֳ�3�����������Σ����ǰ��������߶ν�����������ε������ߣ�
��1��������ͼ2�������ֲ�ͬ�ķ�����������Ϊ45��ĵ��������ε������ߣ�����עÿ�����������ζ��ǵĶ������������ַ����ֵõ������γ�3��ȫ�������Σ�����Ϊͬһ�֣�
��2����ABC�У���B=30�㣬AD��DE�ǡ�ABC�������ߣ���D��BC���ϣ���E��AC���ϣ���AD=BD��DE=CE�����C=x�㣬�Ի���ʾ��ͼ�������x���п��ܵ�ֵ��
��3����ͼ3����ABC�У�AC=2��BC=3����C=2��B���뻭����ABC�������ߣ�����������ߵij���
���𰸡�
��1���⣺��ͼ2��ͼ��

��2���⣺��ͼ3 �١�������ABC��

�ٵ�AD=AEʱ��
��2x+x=30+30��
��x=20��
�ڵ�AD=DEʱ��
��30+30+2x+x=180��
��x=40��
���ԡ�C�Ķ�����20���40��
��3���⣺��ͼ4��CD��AE��������������ߣ�

���B=�������DCB=��DCA=��EAC=������ADE=��AED=2����
��ʱ��AEC�ס�BDC����ACD�ס�ABC��
��AE=AD=x��BD=CD=y��
�ߡ�AEC�ס�BDC��
��x��y=2��3��
�ߡ�ACD�ס�ABC��
��2��x=��x+y����2��
���������÷����� ![]() ��
��
���  ��
��
�������߳��ֱ��� ![]() ��
�� ![]() ��
��
����������1��45����Ȼ�뵽����ֱ�������Σ�����һ�������Աߵĸߣ������γ�һ������ֱ�������κ�ֱ�������Σ�ֱ��������б�ߵ����߿��γ��������������Σ�����һ��������ڶ������ο��Կ��������и����ķ���������ͬ����һ����Ϊ�µ��������εĵǣ�����һ�ű���Ϊ45���22.5�㣬����22.5��ֱ���Ϊ���������εĵǻǣ���������Ϊ��ʱ���õ�����������ǡ��Ϊ���������Σ�����һ��������������2������������ֱ�߱���30��ǣ�����ȷ��һ��ΪBA��һ��ΪBC��������������ȹ̶�BA�ij��������ȷ��D�㣬�ٱ���ͼʵ�驁���ֱ���ADΪ���������ε������ߵױߣ����A��E��C��ͬһֱ���ϣ���2��������ABC������ͼ����x��ֵ����3����Ϊ��C=2��B������C�Ľ�ƽ���ߣ���ɵõ�һ�����������Σ��������Բ�棬�Ա߳����������ݽ��㣬Ѱ���Ƿ���������ߣ�����ͼ4ͼ��Ϊ�����ߣ���ɸ�����ǵ����ڽ�֮�ͼ�����ȵ�����г�������ϵ����ⷽ�̿�֪���ߵij���


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����������������������ù������г����ﳵʱ��t����λ���֣�������õ����ݷֳ����飬��������ͼͳ��ͼ�������ͼ����Ϣ������������⣺
��1����α�������������Ƕ��٣�
��2�������ʾA�������Բ�ĽǵĶ���������ȫ����ͳ��ͼ��
��3����������г���ƽ���ٶ�Ϊ12km/h������㣬�����ù������г��������У��ﳵ·�̲�����6km��������ռ�İٷֱȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������ڶ�����Ĺ�·l����ʻ��;��A��B��C��D�ĸ�ʮ��·�ڶ��к��̵ƣ�AB֮��ľ���Ϊ800�ף�BCΪ1000�ף�CDΪ1400�ף���l�ϸ�·�ڵĺ��̵�����Ϊ��ͬʱ����ƻ�ͬʱ���̵ƣ�ÿ�κ죨�̣�������ʱ����ͬ���������ʱ�����̵�����ʱ��Ҳ��ͬ�����̵Ƹ���ʱ����������A·����ÿСʱ30ǧ���ٶ���l����ʻ��ͬʱ��������D·������ͬ���ٶ���l������ʻ������������ͨ���ĸ�·��ʱ��û��������ƣ���ÿ���̵�����ʱ���������Ϊ�� �� 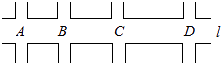
A.50��
B.45��
C.40��
D.35��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧ��ͳ��֪ʶ��С�վͱ���ͬѧ��ѧ��ϲ���ij��з�ʽ��������һ�ε��飮ͼ��1����ͼ��2���������ݲɼ������ݻ��Ƶ�������������ͳ��ͼ�������ͼ���ṩ����Ϣ����������⣺ 
��1����ȫ����ͳ��ͼ������������ﳵ����������Ӧ��Բ�ĽǵĶ�����
��2�����ȫ�꼶��600��ͬѧ�������ȫ�꼶������ѧ��ѧ��������
��3������3����ϲ���˳�����ѧ����1����ϲ�����С���ѧ����1����ϲ���ﳵ����ѧ����Ӳμ�һ����������ѡ��2�˵����鳤���������������г����п��ܵ�����������2�˶��ǡ�ϲ���˳�����ѧ���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Ϊ��������������ʵ��֮һ�Ĺ������г����蹤���ѻ�����ɣ�ij���ŶԽ���4�·��е�7������˹������г��������ͳ�ƣ������ͼ�� 
��1������7�����������������λ����ƽ������
��2���ã�1���е�ƽ��������4�·ݣ�30�죩��������Σ�
��3���������ڹ������г�������Ŀ�й�Ͷ��9600��Ԫ������2014�깲�3200�Σ�ÿ����ƽ���������0.1Ԫ����2014���������ռ��Ͷ��İٷ��ʣ���ȷ��0.1%����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�D��AB�е㣬����CD�� 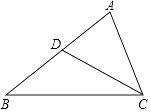
��1����AB=10�ҡ�ACD=��B����AC�ij���
��2����D����BC��ƽ���߽�AC�ڵ�E���� ![]() =
= ![]() ��
�� ![]() =
= ![]() ����������
���������� ![]() ��
�� ![]() ��ʾ
��ʾ ![]() ��
�� ![]() ��ֱ��д�������
��ֱ��д�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC�У�AB=AC=3��BC=2����D�DZ�AB�ϵĶ��㣬����D��DE��BC������AC�ڵ�E����Q���߶�DE�ϵĵ㣬��QE=2DQ������BQ���ӳ�������AC�ڵ�P����BD=x��AP=y�� 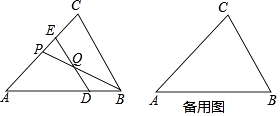
��1����y����x�ĺ�������ʽ��������
��2������PQE�ǵ���������ʱ����BD�ij���
��3������CQ������CQB�͡�CBD����ʱ����x��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ΪA��2����1���������߾�����B��0��3������x�ύ��C��D���㣨��C�ڵ�D����ࣩ�� 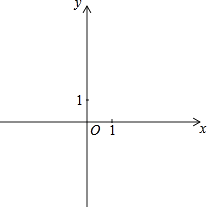
��1�������������ߵı���ʽ��
��2������AB��BD��DA�����ABD�������
��3����P��x���������ϣ������APB=45�㣬���P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ڡ�ABC�У�AB=AC��tan��B=2��BC=4��DΪBC�ߵ��е㣬��E��BC�ߵ��ӳ����ϣ���CE=BC������AE��FΪ�߶�AE���е� 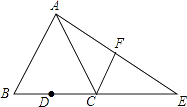
��1�����߶�CF�ij���
��2�����CAE������ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com